. Actas de Ciberseguridad para la Industria 5.0

Actas de Ciberseguridad para
la Industria 5.0

UN VISTAZO A LA TOKENIZACIÓN

Daniel Ayala Zamorano, Laura Natalia Borbolla Palacios, Ricardo Quezada Figueroa, Sandra Díaz-Santiago
Instituto Politécnico Nacional, ESCOM
Ciudad de México, México
{daz23ayala, ln.borbolla.42, qf7.ricardo, sdiazs}@gmail.com

Resumen— Un mecanismo alternativo para proteger datos sensibles, tales como los números de tarjetas bancarias, es la tokenización: consiste en reemplazar la información sensible por valores sustitutos llamados tokens. Al utilizar este mecanismo, se afirma que no es posible recuperar el dato original a partir del token; es decir, no se requiere de ningún mecanismo de seguridad para proteger a los tokens y, por tanto, si un atacante tiene acceso a ellos, no obtendrá ventaja alguna. Aunque esta solución resulta ideal, es necesario analizar, en términos de eficiencia y seguridad, cuáles son las opciones más adecuadas para generar tokens. Hasta el momento, se han propuesto varios algoritmos para hacerlo; sin embargo, no se tiene un análisis comparativo entre los mismos. En este artículo se explica en qué consiste la tokenización, cuáles son los algoritmos existentes para generar tokens y se muestra una comparación de desempeño con base en una implementación propia de estos. Finalmente, es importante señalar que los algoritmos analizados están basados en primitivas criptográficas cuya seguridad ya ha sido probada.

Palabras clave—tokenización, criptografía simétrica, seguridad web

I. INTRODUCCIÓN

Cuando el comercio a través de Internet comenzó a popularizarse, los fraudes de tarjetas bancarias se convirtieron en un problema alarmante: según [13], en 2001 se tuvieron pérdidas de 1.7 mil millones de dólares y para 2002 aumentaron a 2.1 mil millones. En este contexto, el Payment Card Industry Security Standard Council (PCI SSC), integrado por las principales compañías de tarjetas de crédito, desarrolla el estándar Payment Card Industry Data Security Standard (PCI DSS) [16], con el propósito de especificar mecanismos de seguridad para proteger los datos sensibles de las tarjetas de crédito. Sin embargo, satisfacer los requerimientos establecidos en dicho estándar es sumamente difícil, especialmente para los negocios pequeños y medianos. Esto se debe a que la información sensible debe protegerse en donde sea que se encuentre: al almacenarla, transmitirla y/o procesarla. A pesar de la publicación del estándar en 2004, las grandes filtraciones de datos no han cesado: TJX en 2006, Hannaford Bros. En 2008, Target en 2013 y Home Depot en 2014, por mencionar algunos ejemplos [13].

Ante este escenario surge un nuevo paradigma, denominado tokenización, el cual consiste en reemplazar los datos sensibles por un token, es decir, un valor numérico o alfabético que no tiene relación alguna con el dato original. En este paradigma, la información se concentra en un solo lugar para hacer la tarea de protección más sencilla; así, cuando se ingresa un nuevo valor, v.g. un número de tarjeta de un usuario, se genera un token ligado a esa información, el cual se usa en todo el sistema y la información confidencial se protege en un solo lugar. Un posible adversario con acceso a los tokens no podrá obtener la información sensible a partir de estos.

Una de las ventajas de la tokenización es que puede verse como un sistema autónomo, independiente al sistema principal; de esta manera se establece una separación de responsabilidades: el sistema principal realiza la operación del negocio (por ejemplo, una tienda en línea) y el sistema tokenizador se dedica a la protección de la información sensible. Hoy en día, varias compañías ofrecen servicios de tokenización que permiten que los comerciantes se liberen casi por completo de cumplir con el PCI DSS. En la Figura 1, se muestra una distribución bastante común para un comercio en línea: el sistema tokenizador guarda la información sensible en su base de datos y se encarga de realizar las transacciones bancarias.

Aunque esta solución parece apropiada, aún es necesario responder preguntas tales como ¿cuáles son los mecanismos para generar tokens?, ¿cuál es su nivel de desempeño?, ¿cuáles son las implicaciones de seguridad al utilizar algún algoritmo en particular? Desafortunadamente, la tokenización se ha visto rodeada por una nube de desinformación desde sus inicios; la falta de una definición formal permitió que las campañas publicitarias de las empresas tokenizadoras difundieran información imprecisa: se suele mencionar que la tokenización y la criptografía no están relacionadas directamente, o bien, que la primera es una alternativa (y no una aplicación) de la segunda. Por ejemplo, lo único que Shift4 dice con claridad sobre sus tokens, es que se trata de valores aleatorios, únicos y alfanuméricos [19]; para Braintree, la única manera de generar tokens es por métodos aleatorios [6]; finalmente, para Securosis los tokens son valores aleatorios que nada tienen que ver con la criptografía [18]; es fácil observar que la mayoría de las empresas trata a sus métodos como secretos de compañía, esperando que el trato entre cliente y proveedor esté basado en la confianza y no en la comparación de los propios métodos tokenizadores.

Afortunadamente, ya se han dado los primeros pasos para responder a las preguntas antes planteadas. Hasta el momento se han propuesto diversas soluciones para generar tokens, las cuales están basadas en primitivas criptográficas y también se ha comenzado a analizar la seguridad de tales soluciones. El presente artículo ofrece una breve descripción de los principales algoritmos para generar tokens, los cuales están basados en funciones hash, cifrados por bloque, cifrados que preservan el formato, entre otros. También se analiza la eficiencia de los mismos, con la finalidad de ofrecer un punto de comparación entre ellos.


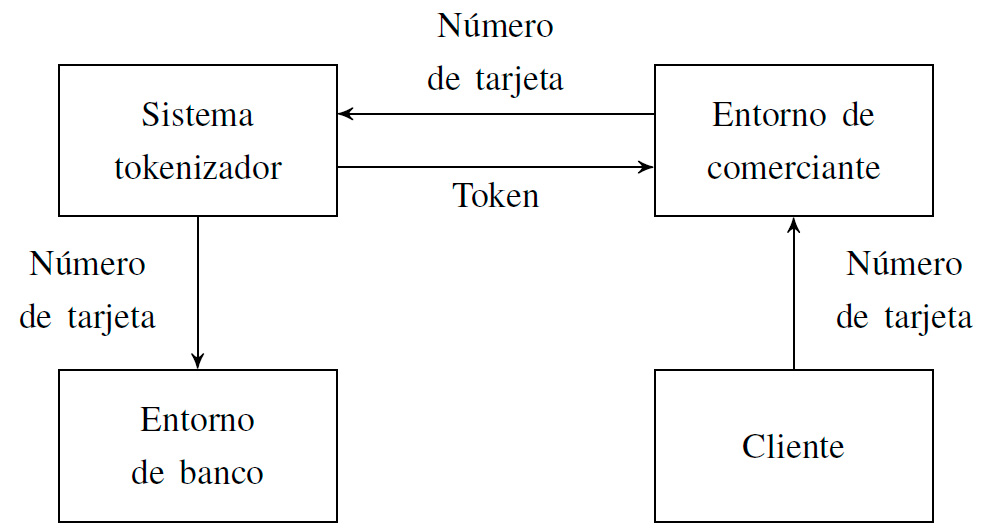
Figura 1. Arquitectura típica de un sistema tokenizador.


En la Sección II se definen las primitivas criptográficas que utilizan los distintos algoritmos para generar tokens; en la Sección III, se da una breve descripción de los métodos de tokenización implementados. Finalmente, en la Sección IV, se presentan los resultados de las comparaciones de desempeño realizadas y se concluye con una discusión alrededor del tema.

II. PRELIMINARES

II-A. Notación

Se denotará a todas las cadenas de bits de longitud n como {0, 1}n y a las cadenas de longitud arbitraria como {0, 1}*.Para una cadena de símbolos x sobre un alfabeto arbitrario, |x| simboliza la longitud de la cadena.

II-B. Primitivas criptográficas

Un cifrado por bloques se define como una función e : M × K → C donde M = C = {0, 1}n, K = {0, 1}k, n, es el tamaño del bloque y k, el tamaño de la llave [14].

Los modos de operación permiten extender la funcionalidad de los cifrados por bloque para poder operar sobre bloques de información de tamaño arbitrario. Más formalmente, un modo de operación es un procedimiento que recibe como entrada un mensaje de longitud arbitraria M ∈ {0, 1}*, una llave K ∈ {0, 1}k, un vector de inicialización IV ∈ {0, 1}v y da como salida un texto cifrado C ∈ {0, 1}* [8].

Una función hash criptográfica asocia cadenas de longitud arbitraria a cadenas de longitud fija: H : {0, 1}* → {0, 1}h, donde h es la longitud de la cadena de salida, también denominada resumen o digesto. No debe ser factible recuperar el mensaje a partir de su valor hash, ni encontrar dos mensajes que produzcan el mismo hash [14].

Un código de autenticación de mensaje (MAC, Message Authentication Code) es una primitiva criptográfica que provee integridad. Se define como una tupla de tres algoritmos: generación de claves, generación de la etiqueta y verificación de la etiqueta. El algoritmo para generar la etiqueta recibe como entrada una llave K ∈ K y un mensaje M ∈ {0, 1}*; como salida se obtiene una etiqueta τ ∈ {0, 1}t. El algoritmo de verificación calcula una etiqueta τ’ a partir del mensaje M y la llave K, y la compara con la etiqueta τ: si ambas son iguales, se dice que el mensaje no ha sido modificado.

Aunque existen varias maneras de generar MAC, en este trabajo solamente se utiliza solamente CBC-MAC [20].

Las redes Feistel son cifrados iterativos que transforman un texto en claro de 2t bits denominado (L0,R0), en donde L0 y R0 son bloques de t bits, en un texto cifrado (Rr,Lr) a través de un proceso de r rondas. Existen dos generalizaciones de este concepto, las redes alternantes y las redes desbalanceadas; ambas permiten modificar el tamaño de las mitades izquierda y derecha: 1 ≤ |Ln| ≤ 2t y |Rn| = 2t − |Ln| [17].

Un cifrado que preserva el formato (en inglés Formatpreserving Encryption, FPE) es un cifrado simétrico en donde el mensaje en claro y el mensaje cifrado mantienen un formato común. Formalmente, de acuerdo a lo definido en [3], se trata de una función E : K × N × T × X → X, en donde los conjuntos K, N, T , X corresponden al espacio de llaves, espacio de formatos, espacio de tweaks y el dominio, respectivamente. El proceso de cifrado de un elemento del dominio con respecto a una llave K, un formato N y un tweak T se escribe como 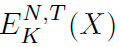. El proceso inverso es también una función D : K × N × T × X → X, en donde .

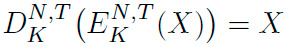III. ALGORITMOS TOKENIZADORES

En el presente artículo se trata a la generación de tokens como un servicio, ver Figura 1, por lo que la interfaz para los procesos de tokenización y detokenización, desde el punto de vista del usuario, se define como sigue: el proceso para generar un token es una función E : X → Y y el proceso para recuperar al número de tarjeta es simplemente la función inversa D : Y → X, en donde X y Y son los espacios de números de tarjetas y tokens, respectivamente. Los números de tarjetas bancarias cuentan con entre 12 y 19 dígitos, y están normados por el estándar ISO/IEC-7812 [12].

III-A. Clasificación del PCI SSC

El PCI SSC establece en sus guías de tokenización la siguiente clasificación para los algoritmos tokenizadores [15]:

  • Métodos reversibles. Aquellos para los cuales es posible obtener el número de tarjeta a partir del token.
    • Criptográficos. El proceso de tokenización está basado en un esquema de cifrado simétrico que usa el número de tarjeta y una llave para obtener un token. El proceso de detokenización solicitará el token y la misma llave para recuperar el número de tarjeta.
    • No criptográficos. Se requiere una base de datos para guardar las relaciones entre números de tarjetas y tokens; el proceso de detokenización es una consulta a la base de datos.
  • Métodos irreversibles. Aquellos en los que no es posible obtener el número de tarjeta original a partir del token.
    • Autenticable. Permiten validar cuando un token dado corresponde a un número de tarjeta.
    • No autenticable. No permiten hacer la validación anterior.

III-B. Algoritmos implementados

En esta sección se describen brevemente algunas de las soluciones que han sido propuestas por la comunidad académica para generar tokens. Las dos primeras son cifrados que preservan el formato que ya forman parte de los estándares del NIST (National Institute of Standards and Technology) [10]. La ventaja de estos mecanismos es que no se requiere de una base de datos para recuperar el número de tarjeta de crédito, basta con descifrar el token.

FFX (Format-preserving Feistel-based Encryption) fue presentado en [4] por Bellare, Rogaway y Spies. Este algoritmo permite cifrar cadenas de cualquier longitud en cualquier alfabeto; en particular, se consideran alfabetos binarios y alfabetos decimales, denominados A2 y A10, respectivamente. FFX A10 usa una red Feistel alternante junto con una adaptación de AES-CBC-MAC (usada como función de ronda) para lograr preservar el formato. Brier, Peyrin y Stern propusieron el algoritmo BPS [7] que se conforma de 2 partes: un cifrado interno BC que cifra bloques de longitud fija y un modo de operación especial, encargado de extender la funcionalidad de BC y de permitir cifrar cadenas de mayor longitud.

En 2016, Díaz et. al. [9] analizaron el problema de la generación de tokens desde el punto de vista criptográfico y propusieron un algoritmo (TKR) que no está basado en cifrados que preservan el formato. Hasta antes de la publicación de este documento, los únicos métodos para generar tokens cuya seguridad estaba formalmente demostrada eran los basados en cifrados que preservan el formato. El algoritmo propuesto usa un cifrado por bloques para generar tokens pseudoaleatorios y almacena en una base de datos la relación original de estos con los números de tarjetas. El proceso de detokenización es simplemente una consulta sobre la base de datos.

En 2017, Longo, Aragona y Sala [1] propusieron un algoritmo que denominaron híbrido reversible (AHR) que está basado en un cifrado por bloques y utiliza una base de datos para almacenar las relaciones entre número de tarjeta y token. Las entradas del algoritmo son la parte del número de tarjeta a cifrar y una entrada adicional (por ejemplo, la fecha) que permite que se tengan varios tokens relacionados con la misma tarjeta. Como se desea obtener un token que tenga el mismo número de dígitos que la tarjeta ingresada, se utiliza un método llamado caminata cíclica [5] para asegurarse de que el texto cifrado pertenezca al espacio del texto en claro.

Probablemente el método más directo para generar tokens es mediante un DRBG (Deterministic Random Bit Generator). La idea es producir una cadena binaria aleatoria con un DRBG e interpretarla para que tenga el formato de un token. Para este trabajo se hizo la implementación de dos DRBG: uno basado en funciones hash y otro basado en un cifrado por bloques; ambos definidos en el estándar del NIST 800-90A [2].

El método que utiliza como mecanismo interno a una función hash consiste en ir concatenando de forma consecutiva los valores hash derivados de la semilla e ir incrementando el valor de esta. El método basado en un cifrado por bloques utiliza el modo de operación CTR, en donde la semilla juega el papel de vector de inicialización. En ambos casos, la seguridad se basa en que la semilla sea un valor secreto.


Tabla I COMPARACIÓN DE TIEMPOS DE TOKENIZACIÓN.

  Tokenización (μs) Detokenización (μs)
FFX 83 61
BPS 573 315
TKR 4648 281
AHR 5554 657
DRBG 4649 431

Según la clasificación del PCI DSS, FFX y BPS son algoritmos reversibles criptográficos, ya que al ser cifrados que preservan el formato, funcionan como esquema de cifrado simétrico. TKR, AHR y DRBG son, contradictoriamente, reversibles no criptográficos, pues necesitan de una base de datos para guardar las relaciones tarjeta-token.

IV. RESULTADOS Y CONCLUSIONES

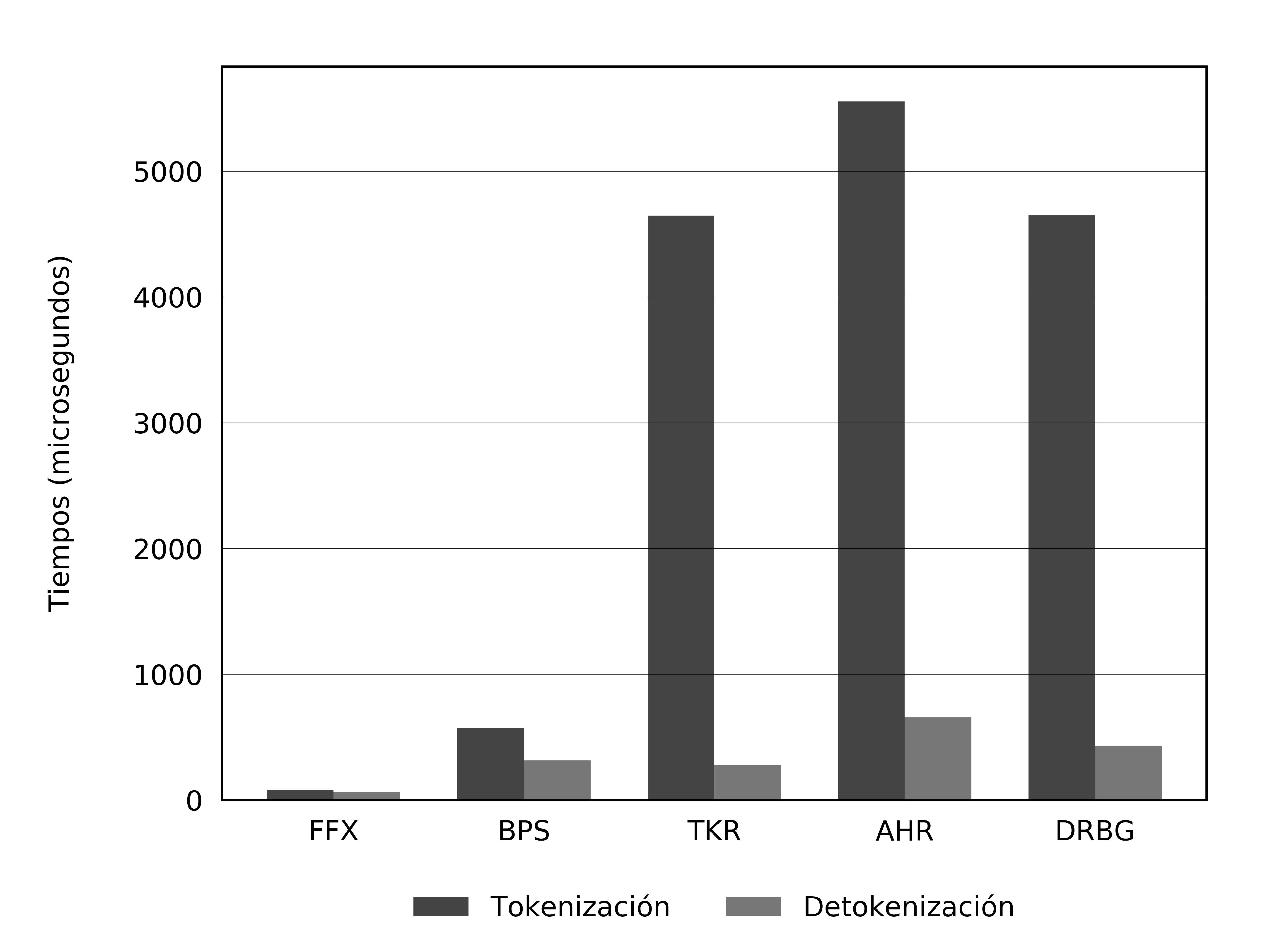
En la Tabla I y la Figura 2a se muestran los resultados en tiempo de las ejecuciones de los algoritmos presentados en la Sección III-B. Estos se llevaron a cabo en una computadora con las siguientes características:

  • Procesador: Intel i5-7200U (2.5 GHz) de 4 núcleos.
  • Sistema operativo: Arch Linux, kernel 4.17.
  • Base de datos: MariaDB 10.1.
  • Compilador: GCC 8.1.1.

El procesador utilizado soporta los conjuntos de instrucciones de Intel AES-NI y RD-SEED [11]. Los algoritmos tokenizadores que usan un cifrado por bloques utilizan una implementación de AES con las instrucciones a nivel de hardware. El DRBG se implementó haciendo uso de la instrucción RD-RAND como fuente de entropía.

La comparación de la Figura 2a muestra como los dos algoritmos reversibles, FFX y BPS, son considerablemente más rápidos que los tres irreversibles: TKR, AHR y DRBG. Los reversibles están en el rango de 60 a 170 microsegundos, mientras que los irreversibles están en alrededor de los 5500 microsegundos. También es posible observar que, para los métodos irreversibles, el proceso de detokenización es mucho más rápido que la generación de tokens. Estos dos resultados dejan ver un poco la carga de las operaciones en los métodos irreversibles: la tokenización involucra una consulta a la base, la generación del token y una inserción; la detokenización solamente es una consulta.

El que FFX y BPS sean más rápidos puede resultar un poco contraintuitivo, pues la generación de tokens reversibles involucra más operaciones; es por esto que en la Figura 2b se muestran los tiempos de la generación de tokens, sin tomar en cuenta tiempos de acceso a base de datos. En este caso, el más veloz es DRBG, seguido de cerca por TKR y AHR; los dos reversibles van al último.

Además de los tiempos de ejecución, también es importante señalar que los irreversibles, al operar como funciones de un solo sentido, son más seguros que los reversibles: un atacante con acceso a la llave de cifrado puede obtener el número de tarjeta correspondiente si se trata de un método reversible, mientras que con un método irreversible necesita también acceso a la base de datos.

La denominación no criptográficos, de la clasificación del PCI DSS resulta totalmente confusa, pues en realidad todos los métodos conocidos que caen en esa categoría utilizan primitivas criptográficas. La segunda categoría (irreversibles) carece de utilidad para aplicaciones que procesan pagos con tarjetas de crédito, pues la habilidad de regresar al número de tarjeta a partir de su token es uno de los requerimientos principales para los sistemas tokenizadores. Por lo anterior, en este trabajo se propone una clasificación distinta:

  • Métodos criptográficos. Todos aquellos basados en primitivas criptográficas.
    • Reversibles. Usan un esquema de cifrado simétrico. El mecanismo de tokenización cifra el número de tarjeta y la detokenización descifra el token para obtener el número de tarjeta original.
    • Irreversibles. Hacen uso de algoritmos criptográficos para generar el token y herramientas externas, como una base de datos, para guardar las relaciones entre tokens y números de tarjetas.
  • Métodos no criptográficos. Aquellos métodos que no necesitan herramientas relacionadas con la criptografía; por ejemplo, un generador de números realmente aleatorio (TRNG, True Random Number Generator).

(a) Tokenización y detokenización

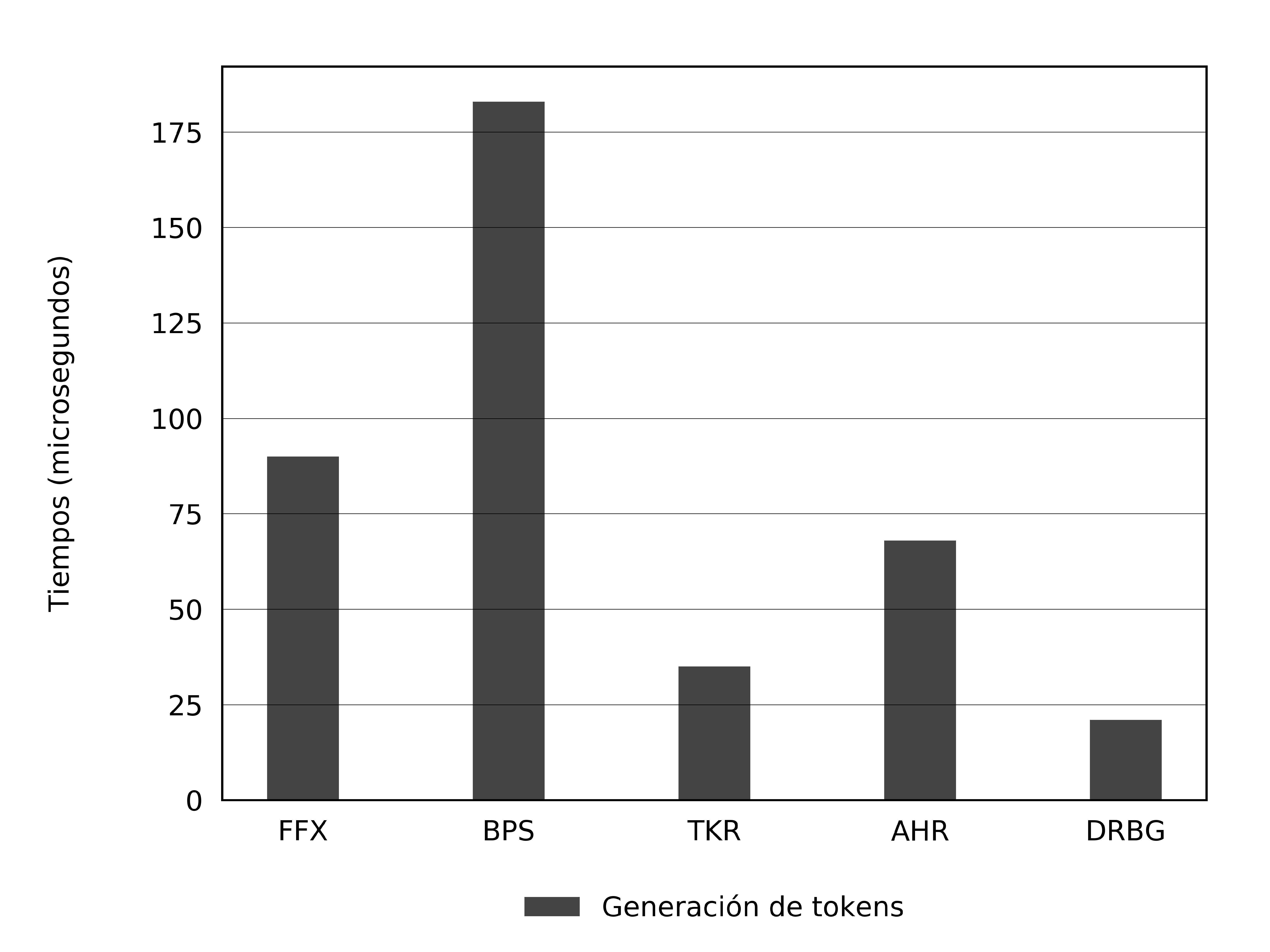
(b) Generación de tokens

Figura 2. Comparaciones de tiempos.


AGRADECIMIENTOS

Los autores agradecen el apoyo del Instituto Politécnico Nacional, a través del proyecto multidisciplinario SIP 1917, módulo 20180775.

REFERENCIAS

  1. [1] R. Aragona, R. Longo, and M. Sala. Several proofs of security for a tokenization algorithm. Appl. Algebra Eng. Commun. Comput., 28(5):425–436, 2017.
  2. [2] E. Barker and J. Kelsey. NIST special publication 800-90a – recommendation for random number generation using deterministic random bit generators, 2015.
  3. [3] M. Bellare, T. Ristenpart, P. Rogaway, and T. Stegers. Format-preserving encryption. In M. J. J. Jr., V. Rijmen, and R. Safavi-Naini, editors, Selected Areas in Cryptography, volume 5867 of Lecture Notes in Computer Science, pages 295–312. Springer, 2009.
  4. [4] M. Bellare, P. Rogaway, and T. Spies. The FFX mode of operation for format-preserving encryption. NIST submission, 2010. http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/ffx/ffx-spec.pdf.
  5. [5] J. Black and P. Rogaway. Ciphers with arbitrary finite domains. In B. Preneel, editor, CT-RSA, volume 2271 of Lecture Notes in Computer Science, pages 114–130. Springer, 2002.
  6. [6] Braintree. Tokenization secures CC data and meet PCI compliance requirements. https://www.braintreepayments.com/blog/using-tokenizationto-secure-credit-card-data-and-meet-pci-compliance-requirements/. Consultado en marzo de 2018.
  7. [7] E. Brier, T. Peyrin, and J. Stern. BPS: a format-preserving encryption proposal. NIST submission, 2010. http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/bps/bps-spec.pdf.
  8. [8] D. Chakraborty and F. Rodríguez-Henríquez. Block cipher modes of operation from a hardware implementation perspective. In Cryptographic Engineering, pages 321–363. 2009.
  9. [9] S. Diaz-Santiago, L. M. Rodríguez-Henríquez, and D. Chakraborty. A cryptographic study of tokenization systems. Int. J. Inf. Sec., 15(4):413–432, 2016.
  10. [10] M. Dworkin. NIST special publication 800-38g – recommendation for block cipher modes of operation: Methods for format-preserving encryption, 2016.
  11. [11] G. Hofemeier and R. Chesebrough. Introduction to intel AES-NI and intel secure key instructions.
  12. [12] International Organization for Standarization. ISO/IEC 7812. 5 edition, 2017.
  13. [13] J. S. Kiernan. Credit card and debit card fraud statistics. https:// wallethub.com/edu/credit-debit-card-fraud-statistics/25725/. Consultado en marzo de 2018.
  14. [14] A. Menezes, P. C. van Oorschot, and S. A. Vanstone. Handbook of Applied Cryptography. CRC Press, 1996.
  15. [15] Payment Card Industry Security Standards Council. Tokenization product security guidelines – irreversible and reversible tokens, 2015.
  16. [16] Payment Card Industry Security Standards Council. Data security standard - version 3.2, 2016.
  17. [17] B. Schneier and J. Kelsey. Unbalanced feistel networks and block cipher design. In Fast Software Encryption, Third International Workshop, Cambridge, UK, February 21-23, 1996, Proceedings, pages 121–144, 1996.
  18. [18] Securosis. Understanding and selecting a tokenization solution. https://securosis.com/assets/library/reports/Securosis_Understanding_Tokenization_V._.1_.0_.pdf. Consultado en febrero de 2018.
  19. [19] Shift4 Payments. The history of truetokenization. https://www.shift4.com/dotn/4tify/trueTokenization.cfm. Consultado en agosto de 2018.
  20. [20] D. Whiting, R. Housley, and N. Ferguson. Counter with CBC-MAC (CCM). RFC, 3610:1–26, 2003.
  • ISSN: 3061-8991
  • Vol 1, 2025