Actas de Ciberseguridad para la Industria 5.0

SISTEMA DE CIFRADO ROBUSTO PARA IMÁGENES DIGITALES BASADO EN AUTÓMATAS CELULARES Y S-BOX

Juan José Contreras Torres¹, Marco Tulio Ramírez Torres¹, Ricardo Eliu Lozoya Ponce², Jesús Agustín Aboytes González³

¹Coordinación Académica Región Altiplano Oeste Universidad Autónoma de S L. P. Salinas, Mexico,
juanjosetorres96@outlook.com, tulio.torres@uaslp.mx

²Academia de Ingeniería Universidad de Guadalajara, Guadalajara, México,
rlozoya@academicos.udg.mx

³Instituto de Investigación en Comunicación Óptica Universidad Autónoma de S L. P. San Luis Potosí, México
agustin.aboytes@upslp.edu.mx

Abstract—En esta investigación se presenta la implementación y validación de un sistema de cifrado de imágenes digitales. Este sistema busca proporcionar seguridad criptográfica y perceptual a imágenes que posean una alta redundancia de datos, utilizando cajas de sustitución y autómatas celulares. Las cajas de sustitución son diseñadas bajo diversos criterios con el fin de superar los ataques de criptoanálisis y cumplir con el criterio Avalanche. El problema al usar cajas de sustitución radica cuando el texto plano es altamente redundante, porque la sustitución se realiza siempre por el mismo valor, dejando notar patrones de la imagen original. Por otro lado, la sincronización de autómatas celulares ha demostrado ser sensible a condiciones iniciales al grado que puede usarse para diseñar generadores de números pseudoaleatorios. Por lo tanto en este sistema se combinan ambas técnicas para lograr un sistema seguro y robusto para el cifrado de imágenes.

Keywords— autómatas celulares, cifrado, S-box.

I. INTRODUCCION

Cada vez es más frecuente que podamos realizar más operaciones vía internet, facilitando así los procesos y optimizando tiempos. Sin embargo, esto requiere brindar seguridad a los usuarios, dado que sus datos se encuentran expuestos en las transmisiones o en el lugar de almacenamiento. Una de las técnicas empleadas para proteger información son los algoritmos criptográficos. Esta técnica consiste en volver ininteligible la información, de forma tal que solo pueda ser recuperada utilizando la clave correcta.

En la actualidad el cifrado de imágenes es un campo de investigación muy activo, debido a las múltiples áreas donde se requiere, por ejemplo: en el servicio de televisión de paga, sistemas de imagen médica, videoconferencias, comunicaciones militares, video vigilancia, entre otras. A pesar de que se cuenta con varios algoritmos de cifrado convencionales, como lo son AES (Advanced Encryption Standard), DES (Data Encryption Standard) e IDEA (International Data Encryption Algorithm), han resultado en muchas ocasiones imprácticos para el cifrado de imágenes, debido a las propiedades intrínsecas de éstas, tales como una gran tasa de datos, una fuerte correlación adyacente, una alta redundancia, entre otras [1]. Por lo tanto, el problema de seguridad se extiende debido a que los algoritmos para cifrado de imágenes deben brindar seguridad perceptual y seguridad criptográfica.

Lo anterior ha fomentado la búsqueda e implementación de nuevos esquemas de cifrado de imágenes, como lo son los sistemas de cifrado con enfoque caótico. Es por eso que en esta investigación se conjunta la sincronización de autómatas celulares basada en la regla 90, la cual es de dinámica caótica discreta y las cajas de sustitución (S-box) para brindar un algoritmo fuerte contra ataques de criptoanálisis diferencial y estadísticos. El artículo se compone de la siguiente manera, en el capítulo 2 se describe el marco teórico y el método de cifrado, mientras que en el capítulo 3 se muestran los resultados obtenidos en distintas pruebas de seguridad. El capítulo 4 contienen las conclusiones de la investigación.

II. ANTECEDENTES

A. Autómatas celulares

El concepto de autómata celular (AC) fue introducido en la década de los años 40 por el matemático John von Neumann y Stanislaw Ulam [2]. Los AC son usados para modelar comportamientos complejos donde se involucran interacciones locales. De hecho, los AC representan una clase de sistemas dinámicos capaces de describir la evolución de sistemas utilizando reglas simples, sin la necesidad de utilizar ecuaciones diferenciales.

Los autómatas celulares consisten en un conjunto ordenado de celdas, en forma de rejilla, donde cada celda tiene un número finito de estados. Los autómatas celulares forman una rejilla de dos dimensiones, donde sus celdas evolucionan en pasos discretos acorde a una regla local de actualización aplicada de manera uniforme, sobre todas las celdas. En el inicio, un estado es asignado a las celdas en el tiempo t=0, donde los nuevos estados de la celda dependerán de sus estados previos y los de su vecindad, como se muestra en Fig. 1.

Los autómatas celulares elementales (ACE) son AC de una dimensión, con dos estados y de vecindad de radio 1. Una regla local de autómatas celulares es el algoritmo usado para calcular el siguiente estado de la celda. Los ACE difieren entre sí, solo por la elección de la regla local, contienen solo tres variables (celdas) y cada una puede tomar solo dos valores (1,0), por lo tanto existen solo 8 combinaciones, resultando 2⁸=256 reglas locales y ACE diferentes. Por ejemplo, la regla local 90 es descrita por la siguiente expresión:

(1)

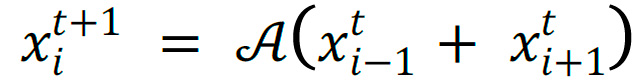
El fenómeno de sincronización ocurre cuando después de un periodo de tiempo, los comportamientos de dos sistemas dinámicos se aproximan arbitrariamente. En el caso de AC, después de un número de pasos en el tiempo t, la diferencia entre los vectores x y y correspondientes al autómata celular controlador y replica respectivamente, eventualmente resultará el vector nulo 0= (0,0….0). Para esto es necesario que en cada paso, ambos vectores evolucionen usando la misma regla local.

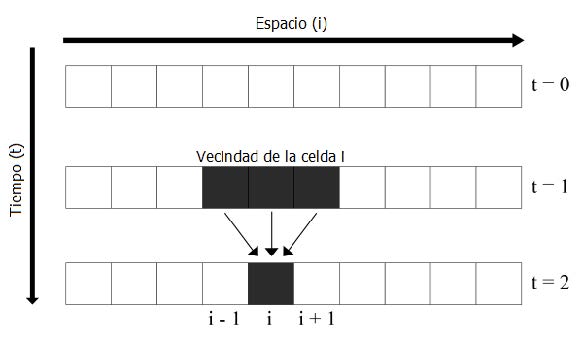
Fig. 1. Diagrama espacio-tiempo de un automata celular

En la referencia [3] se demostró que un par de ACE que evolucionan utilizando la regla local 90, sincronizan si las coordenadas acopladas están separadas por un bloque de N=2ⁿ-1 sitios desacoplados, siendo n un entero positivo. Basado en el fenómeno de sincronización, en [4] los autores propusieron un Generador de Números Pseudo-Aleatorios (GNPA). La función principal es llamada h, y requiere dos vectores x y y de n bits y n+1 bits respectivamente. Para calcular una secuencia pseudo-aleatoria, la función requiere que el autómata celular evolucione hacia atrás. Tal situación es descrita en la Fig. 2, donde las compuertas XOR son representadas con los círculos que en medio tienen una cruz, la conectividad de éstas representan la regla local 90, y el vector resultante es llamado vector t.

En la referencia [5] se creó una función de preprocesmiento para intercambiar los valores del texto en claro, basada en el generador de números pseudo-aleatorios, haciendo una modificación en su retroalimentación, ver Fig. 3. El proceso aplicado a imágenes consiste en recibir cada coeficiente de pixel como si fuera el vector x, el vector y será sustituido después de cada iteración por el vector m resultante, concatenando el bit menos significativo del vector y precedente como el bit más significativo del nuevo vector. Esta función permite romper la alta correlación adyacente de las imágenes, permitiendo una sustitución dinámica de la información.

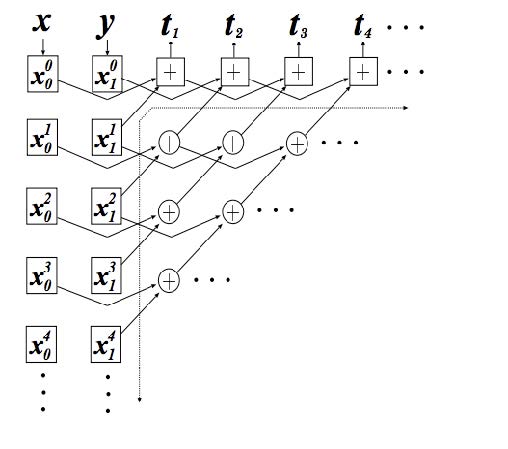
Fig. 2. Generador de secuencias pseudo-aleatorias

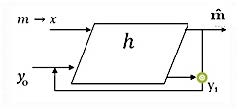
Fig. 3. Función de preprocesamiento basado en la funcin h.

B. S-box

Por otra parte, en la criptografía, las cajas de sustitución son un componente básico en los algoritmos simétricos. La cajas son utilizadas en bloques cifradores para intercambiar el texto en claro y de esta manera ocultar la relación entre la llave de cifrado y el texto cifrado [6].

El diseño y selección de una caja de sustitución es un proceso cuidadoso, porque requiere ser resistente a ataques de criptoanálisis. La Fig. 4 muestra la S-box empleada en el sistema de encriptación AES.

Fig. 4. Caja de sustitucion del sistema AES en notacion hexadecimal.

Por lo tanto, para el desarrollo de este algoritmo de cifrado de imágenes encontramos viable unir ambas herramientas. La operación de preprocesamiento es capaz de romper la alta correlación de las imágenes y las cajas de sustitución proveen de seguridad ante ataques de criptoanálisis diferencial y que cumplen con el criterio Avalanche.

Para incrementar la condición inicial se realizó una nueva versión de la operación de preprocesmiento, donde se utilizan tres operaciones h. Ver Fig. 5.

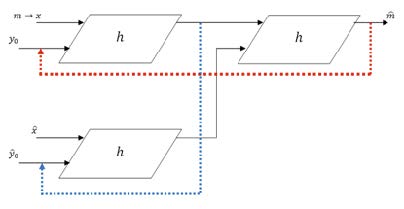
Fig. 5. Función de procesamiento mejorado con tres funciones h.

El algoritmo para cifrar una imagen funciona de la siguiente manera:

1º Se toman bloques de texto en claro de 24 bits (3 pixeles en escala de grises)

2º Se aplica el preprocesamiento a todos los bloques de la imagen.

3º Después se sustituye el valor de cada pixel utilizando una S-box

4º Posteriormente se invierten las columnas y los renglones de la imagen resultante de forma tal que el pixel (n,n) ocupe ahora el lugar (0,0).

5º Finalmente se utiliza otra vez la función de preprocesamiento con la imagen transformada.

La llave secreta de este algoritmo es de al menos 148 bits ya que se utilizan dos funciones de preprocesamiento extendidas.

III. RESULTADOS

A continuación se muestran los resultados del análisis de seguridad aplicado a las imágenes cifradas. Se aplicaron diversas pruebas estadísticas, ataques de criptánalisis y el cálculo de los índices NPCR (Number of Changing Pixel Rate) y UACI (Unified Averaged Changed Intensity) para validar los resultados ante ataques de criptoanálisis diferencial.

Para las pruebas, usamos imágenes ampliamente utilizadas en el procesamiento de imágenes con diferente actividad óptica: mandril, Lena y pimientos. Todas en escala de grises a 8 bits y de dimensiones 512 x 512 pixeles. Podemos ver dos de ellas en las Fig. 6a) y 7a).

La primera prueba consiste en el cálculo de histogramas tanto de la imagen en claro como de su versión cifrada. La Fig. 6 muestra el caso de la imagen de Lena, donde podemos ver que el histograma de su versión cifrada es uniforme, ocultando así la redundancia de datos de la imagen original.

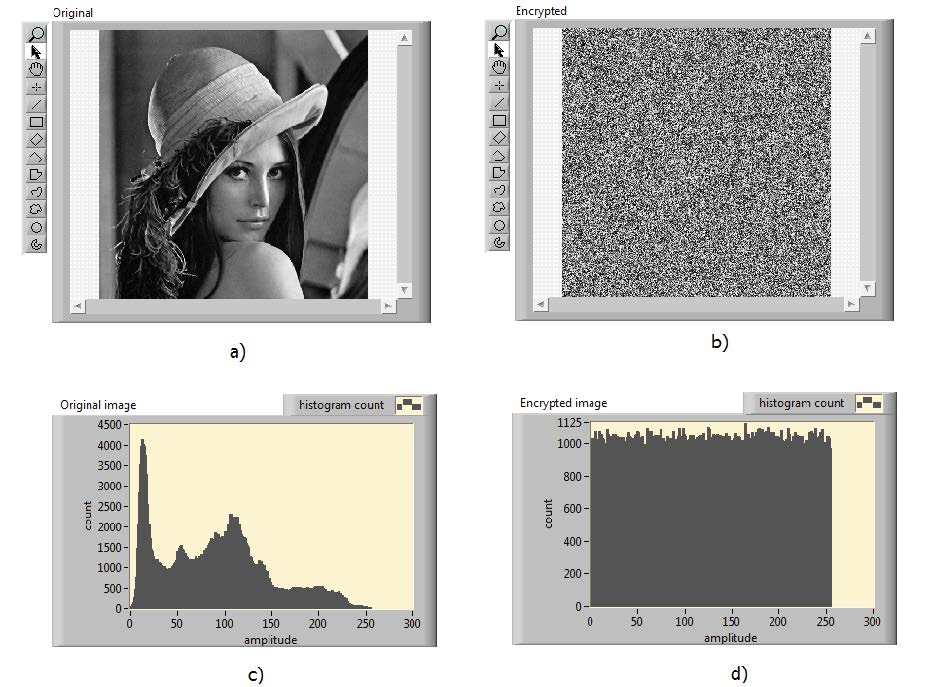
Fig. 6. Análisis de histogramas a) Imagen de Lena, b) Imagen de Lena cifrada, c)Histograma de la imagen original de Lena y d) Histograma de la versión cifrada de Lena.

La segunda prueba que se realizó fue el cálculo del coeficiente de correlación entre las dos imágenes. Esta prueba trata de demostrar la independencia que existe entre la imagen cifrada y la imagen original. Acorde a la interpretación de este valor, sabemos que no existe correlación entre las imágenes si el resultado es próximo a 0. La Tabla 1 muestra los resultados de esta prueba aplicada a las tres imágenes de prueba.

TABLA I. COEFICIENTE DE CORRELACIÓN

Imagen	Coeficiente
Pimientos	-0.0013268
Lena	0.0020740
Mandril	-0.0002453

En el cifrado de imágenes es común analizar la resistencia de los algoritmos ante ataques diferenciales utilizando dos medidas: NPCR y UACI. Ambas mediciones están basadas en pequeños cambios en dos imágenes y cifrarlas bajo la misma llave. Para ilustrar esto, asumamos que tenemos dos imágenes cifradas C¹ y C², cuyas imágenes en claro correspondientes tiene solo un pixel diferente entre sí, y ambas han sido cifradas con la misma llave. Los coeficientes en la escala de grises de ambas imágenes en el renglón i y la columna j son señalados como C¹(i, j) y C²(i, j) respectivamente. Los índices NPCR y UACI son definidos en las ecuaciones (2) y (3).

(2)

(3)

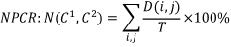
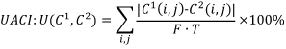
donde D(i, j) está determinado de la siguiente manera: si C¹(i,j) = C²(i, j), entonces D(i, j) = 0, de otra manera D(i, j) = 1, T es el total de pixeles de las imágenes y F denota el valor máximo valido en el formato de la imagen. Para imágenes en escala de grises a 256 niveles, los valores teóricos son UACI=33.464% y NPCR=99.609%, ver [7]. Los resultados obtenidos para nuestro algoritmo se muestran en la Tabla II, donde se cambió el bit menos significativo del pixel del reglón y columna 255.

TABLA II. NPCR Y UACI

Imagen	NPCR	UACI
Pimientos	99.6235%	33.434992%
Lena	99.6021%	33.425587%
Mandril	99.6128%	33.361058%

Como se puede observar en la mayoría de las ocasiones se sobrepasan los valores teóricos y en los casos donde son menores, se encuentran dentro del rango de valores críticos, acorde a [7]. Gracias al 4º paso del algoritmo, sin importar que pixel se modifique, el sistema siempre pasa la prueba.

Por último, realizamos el ataque Chosen-plainimage attack (CPIA). En la referencia [8] señalan que si un criptosistema es seguro contra el ataque CPIA, también es seguro contra otros ataques de criptoanálisis tales como cipherimage-only attack o known-plainimage attack. Este ataque implica que el adversario es capaz de escoger las imágenes en claro y obtener su respectiva versión cifrada, pero no conoce la llave secreta. El ataque comienza seleccionando las imágenes a cifrar, como se puede ver en la Fig. 7, se utilizan la imagen de los pimientos, Fig. 7a) y una imagen negra sólida, Fig. 7c). Ambas imágenes son cifradas bajo la misma llave secreta, los resultados son Fig. 7b) y 7d). Por último, se realiza una operación XOR pixel a pixel entre ambas imágenes cifradas, el resultado será lo que se denomina imagen recuperada, Fig. 7e). Como podemos observar en nuestro caso la imagen resultante no revela información de la imagen original.

Fig. 7. Chosen-plainimage attack aplicado a la imagen de prueba de los pimientos. a) Imagen original, b) imagen cifrada de los pimientos, c) imagen solida escogida, d) imagen máscara y e) la imagen recuperada.

Para corroborar que no existe relación entre la imagen recuperada y la imagen original calculamos nuevamente el coeficiente de correlación entre ambas imágenes. Los resultados se muestran en la Tabla 3.

TABLA III. COEFICIENTE DE CORRELACIÓN

Imagen	Coeficiente
Pimientos	-0.0064724
Lena	0.0046168
Mandril	0.0081693

IV. CONCLUSIONES

En el presente trabajo se propuso un algoritmo para el cifrado de imágenes que, sin importar el nivel óptico de actividad, fuera capaz de ofrecer seguridad criptográfica y perceptual. Ambas herramientas, la sincronización de autómatas celulares y las cajas de sustitución se complementan para cifrar de manera segura esta información.

Como se puede observar en cada una de las pruebas, el algoritmo propuesto pasó de manera exitosa cada una de ellas. La condición inicial o llave de secreta es de 145 bits, por lo tanto, dado el procesamiento actual no es susceptible a romperse utilizando fuerza bruta [9].

V. AGRADECIMIENTOS

M. T. Ramírez-Torres agradece el apoyo recibido por el Proyecto FAI-UASLP con número de registro C18-FAI-05-55.55. Y al PFCE por el apoyo otorgado a la CARAO en el recurso P/PFCE 2018-24MSU0011E22.

REFERENCIAS

[1] S. Lian. Multimedia content encryption: Techniques and applications. New York: Auerbach Publications, 2009.
[2] J. von Neuman. Theory of Self-Reproducing Automata. Urbana: University of Illinois Press, 1996.
[3] J. Urías, E. Ugalde, G. Salazar, “Synchronization of cellular automaton pairs,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 8(4), pp. 814–818, November 1998.
[4] J. Urías, E. Ugalde, G. Salazar, “A cryptosystem based on celular automata,” Chaos: An Interdisciplinary Journal of Nonlinear Science, Vol. 8(4). 819–822, November 1998.
[5] M. T. Ramírez-Torres, J. S. Murguía, M. Carlos Mejía, “Image encryption with an improved cryptosystem based on a matrix approach,” IJMP C, vol. 25, no. 10, p. 1450054, April 2014.
[6] J. Chandrasekaran, B. Subramanyan & R. Selvanayagam, “A chaos based approach for improving non linearity in S box design of symmetric key cryptosystems,” in International Conference on Computer Science and Information Technology, Bangalore, pp. 516-522, Janaury 2011.
[7] Y. Wu, J. P. Noonan, S. Agaian, “NPCR and UACI randomness tests for image encryption,” Cyber journals: multidisciplinary journals in science and technology, JSAT, 2011, vol. 1, no. 2, pp. 31-38, April 2011.
[8] A. M. del Rey, G. R. Sánchez & A. De La Villa Cuenca “Encrypting digital images using cellular automata” in International Conference on Hybrid Artificial Intelligence Systems, Salamanca, pp. 78-88, March 2012.
[9] C. Paar and J. Pelzl. Understanding cryptography: a textbook for students and practitioners. New York: Springer-Verlag, 2010.

ISSN: 3061-8991
Vol 1, 2025