APLICACIÓN A LA CRIPTOGRAFÍA DE SISTEMAS CAÓTICOS LINEALES POR PEDAZOS MEDIANTE EL AUMENTO DE PUNTOS DE EQUILIBRIO
González Del Río Juan Daniel, Ontañón-García Pimentel Luis Javier, Ramírez Torres Marco Tulio
Coordinación Académica Región Altiplano Oeste, Universidad Autónoma de San Luis Potosí, Kilómetro 1 Carretera a Santo Domingo, 78600, Salinas de Hidalgo, San Luis Potosí, México,
j.danielgr18@hotmail.com, luis.ontanon@uaslp.mx, tulio.torres@uaslp.mx
Resumen—En este trabajo de investigación se realizó el estudio y aplicación de sistemas caóticos basados en el uso de sistemas lineales por pedazos, los cuales pueden ser una gran contribución a la encriptación de datos debido a que estos sistemas son fáciles de implementar y además presentan trayectorias caóticas óptimas para los procesos de encriptación. Para esto se utilizó un análisis de la ubicación de los puntos de equilibrio y número de enroscados, con la finalidad de generar un sistema multienroscado. Para el sistema de encriptación se tomó la secuencia dada por el generador como una llave de cifrado y se realizó la unión con los datos de entrada por medio de la operación XOR para producir la encriptación de imágenes en escala de grises. Se efectuó el análisis de seguridad estadístico para determinar la eficiencia del encriptado propuesto y corroborar los datos mediante coeficientes de correlación e histogramas. La cual nos llevará a establecer un sistema de comunicación de video confidencial.
Palabras clave— Encriptación, cifrado de imágenes, sistemas lineales por pedazos, Caos.
I. INTRODUCCIÓN
La idea de transmitir información sensible y ocultarla de manera segura ante posibles intrusos y piratas informáticos, ha generado un impacto muy fuerte en la comunidad científica que inspira a muchos investigadores a combinar una gran variedad de enfoques para abordar este desafiante problema. Varios métodos que enmascaran la información transmitida han sido propuestos durante los últimos años. Estos métodos de encriptación se basan en muchas técnicas diferentes, por ejemplo, encriptación parcial [1], patrones de exploración [2], autómata celular [3,4], entre otros. Una de las áreas que ha comenzado a llamar la atención en la criptografía es el caos. Esto se debe a la dinámica intrínseca de este tipo de sistemas y la relación entre el caos y la criptografía.
Con los crecientes volúmenes de información generada en tiempo real, se necesitan nuevos mecanismos para garantizar la seguridad y evitar el acceso a personas no autorizadas. Los métodos de encriptación convencionales no son apropiados para imágenes, ya que son propensos a ataques estadísticos debido a la fuerte correlación entre píxeles adyacentes y el análisis de histogramas que pueden ayudar a identificarlos dentro de la imagen; con este objetivo en mente, en este trabajo se propone un algoritmo de encriptación mediante el uso de sistemas lineales por pedazos el cual puede llegar a prevenir que una persona no deseada descifre el mensaje encriptado si es que ésta desconoce los parámetros del oscilador usado y las condiciones iniciales del mismo.
En [5], M. García y colaboradores, trabajaron con atractores basados en sistemas lineales por pedazos de diferente número de enroscados, en donde los sistemas y puntos de equilibrio se localizaban únicamente a lo largo del eje 𝑥. Por lo tanto, surge la siguiente pregunta: ¿qué pasaría con la secuencia de la llave cifrada si los enroscados no solo crecieran en el eje 𝑥, sino también en el eje 𝑦? Tomando esto en consideración, en este trabajo de investigación se desarrolla un algoritmo para ubicar puntos de equilibrio en un sistema lineal por pedazos localizados tanto en el eje 𝑥 como en el eje 𝑦, realizando de esta manera un sistema con un mayor número de enroscados que resulte en trayectorias más complejas.
II. DESARROLLO
A. Sistemas caóticos.
La construcción de sistemas dinámicos que muestran un comportamiento caótico es relevante en diversas disciplinas científicas. Por ejemplo, la biología y la meteorología. Estos sistemas modelados matemáticamente por ecuaciones diferenciales ordinarias de primer orden no lineales con parámetros adecuados para garantizar comportamientos caóticos generan atractores extraños. Muchos de los fenómenos no lineales observados en la naturaleza o por el hombre han sido descritos por sistemas caóticos debido a la riqueza de sus comportamientos dinámicos: ciclos límite, órbitas y atractores extraños, etc. Y desde hace algunas décadas, la generación de trayectorias caóticas se ha buscado simplificar con respecto a sus ecuaciones o implementaciones electrónicas. Es por esto por lo que los sistemas lineales por pedazos (PWL) han sido de gran utilidad en este tema. Estos sistemas se basan en parámetros de conmutación que se pueden visualizar como un conjunto de subsistemas y una señal de conmutación que los selecciona durante un intervalo determinado de tiempo.
Para el diseño de trayectorias complejas y caóticas se han implementado sistemas que presenten atractores con múltiples enroscados. Este término, se utiliza para referirse a tres o más enroscados en un atractor visualizado en su espacio de fase. Un enfoque frecuente para generar uno o más enroscados, ha sido el de modificar un sistema que produce originalmente atractores con doble enroscado, como por ejemplo los sistemas de Chua y Lorenz, entre otros, añadiendo puntos de equilibrio al sistema para permitir que el flujo del sistema visite nuevas regiones en el espacio. Los atractores extraños de múltiple enroscado aparecen como resultado de la combinación de varias trayectorias inestables “de una sola espiral" [6].
B. Sistemas lineales por pedazos.
Se consideró el siguiente sistema de ecuaciones dado por:
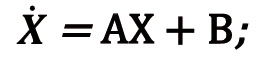
En donde 𝑿 = [𝑥, 𝑦, 𝑧]T representa el vector del estado del sistema, 𝑩 = [𝐵1, 𝐵2, 𝐵3]T ∈ ℝ3 representa un vector real afín. 𝑨 = [𝑎i,j] ∈ ℝ3x3, 𝑖, 𝑗 = 1, 2, 3, denota una matriz real de coeficientes, la cual está dada por:
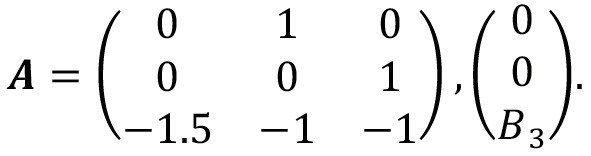
Para este caso en particular consideramos 𝐵1 = 𝐵2 = 0, ya que el punto de equilibrio así se desplazará únicamente en el eje 𝑥. Estamos interesados en un sistema disipativo que tenga un punto de equilibrio hiperbólico en 𝑿∗, y debido a la simplicidad del sistema, estos se pueden calcular mediante 𝑿∗ = −𝐀-𝟏𝐁. En dónde el vector 𝑩 conmutará dependiendo de la posición de 𝑿, de tal forma que para cada valor conmutado en B3 se generará un nuevo punto de equilibrio, tomando la siguiente forma:
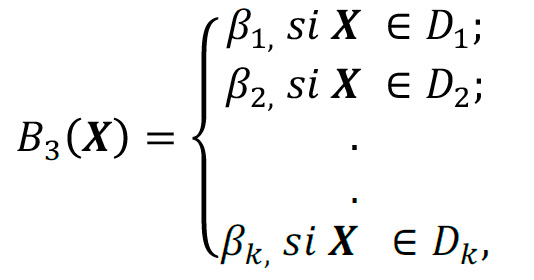
Donde 𝛽
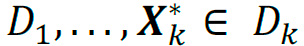con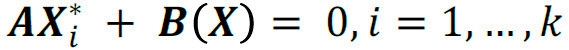 
. El objetivo es elegir valores de 𝛽𝑖, de tal manera que el sistema sea estable y presente enroscados caóticos. En la Fig. 1, se muestra un diagrama de cómo están distribuidos los puntos de equilibrio marcados con puntos negros, los enroscados que se desea obtener mediante línea negra en espiral y las superficies de conmutación tanto del eje 𝑥 como el de 𝑦 marcadas como 𝛼-3 , 𝛼-2 ,…, 𝛼-3 según la región.
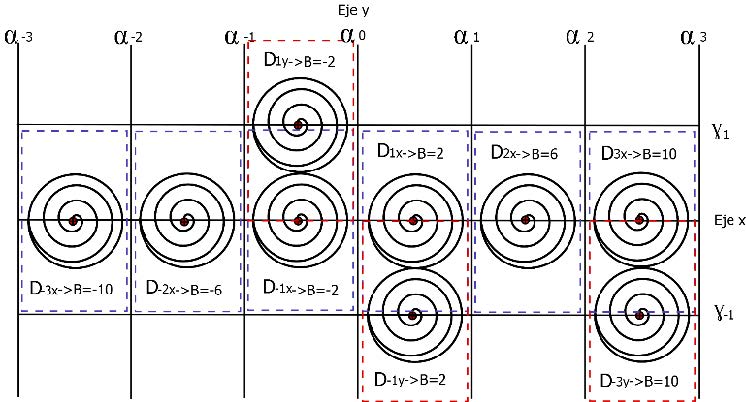
Fig. 1. Diagrama de regiones, superficies de conmutación y colocación de puntos de equilibrio para la realización del sistema multienroscado.
Diagrama de regiones, superficies de conmutación y colocación de puntos de equilibrio para la realización del sistema multienroscado.
La ubicación de estas superficies de conmutación se da a conocer en la Tabla I:
TABLA I. Ubicación de las superficies de conmutación.
| 𝛼0 = 0 | |
| 𝛼-3 = −24/3 | 𝛼3 |
| 𝛼-2 = −16/3 | 𝛼2 |
| 𝛼-1 = −8/3 | 𝛼1 |
| 𝛾-1 = −4/3 | 𝛾1 = 4/3 |
Estos valores se escogieron siguiendo la misma estructura de selección de los puntos de equilibrio que se presentan en [7]. Es importante mencionar que la distribución de estas superficies es simétrica, permitiendo que los enroscados generados presenten las mismas dimensiones. Cada espacio generado entre las superficies de conmutación corresponde con los dominios mencionados en la ec. (3). Para este caso se les asigna el nombre de 𝐷-3𝑥, 𝐷-2𝑥, 𝐷-1𝑥, 𝐷1𝑥, 𝐷2𝑥, 𝐷3𝑥 a los dominios que contienen un punto de equilibrio sobre el eje 𝑥, marcados con las casillas de línea punteada en azul en la Fig. 1. Para el caso de 𝐷-3𝑦, 𝐷-1𝑦, 𝐷1𝑦, marcados en recuadro con línea punteada roja, son los dominios que contienen un punto de equilibrio desplazado tanto en el eje 𝑥 como en el 𝑦.
Dadas estas superficies de conmutación y los dominios en donde se desea la ubicación de los puntos de equilibrio, se diseña la siguiente ley de conmutación para el sistema de la ec. (1) con (2):
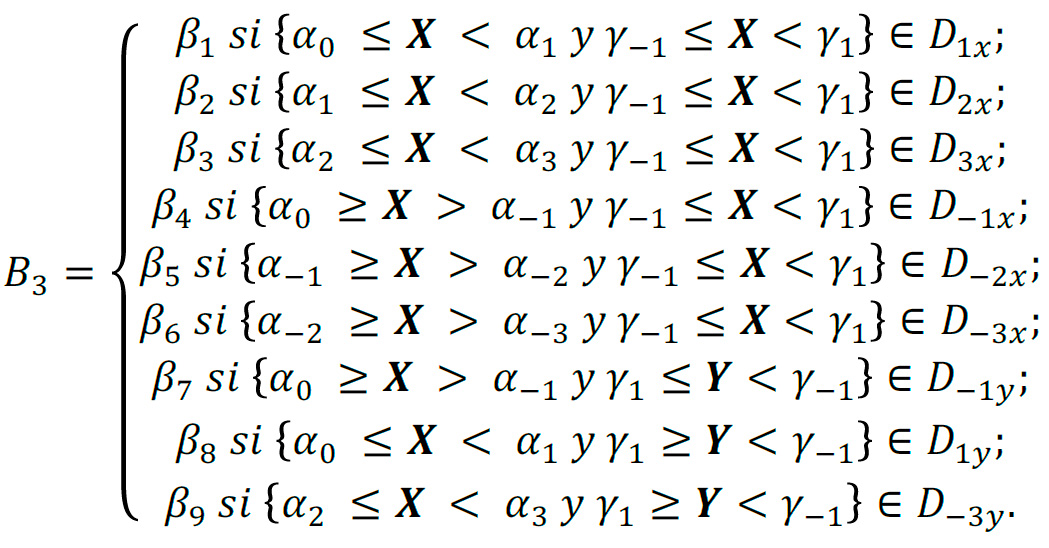
TABLA II. Posición de los puntos de equilibrio para la generación del sistema multienroscado
| Beta | 𝒙 | 𝒚 | 𝒛 |
|---|---|---|---|
| 𝛽1 | 1.333 | 0 | 0 |
| 𝛽2 | 4 | 0 | 0 |
| 𝛽3 | 6.667 | 0 | 0 |
| 𝛽4 | -1.333 | 0 | 0 |
| 𝛽5 | -4 | 0 | 0 |
| 𝛽6 | -6.667 | 0 | 0 |
| 𝛽7 | -1.444 | 2.667 | 0 |
| 𝛽8 | 1.444 | -2.667 | 0 |
| 𝛽9 | 6.778 | -2.667 | 0 |
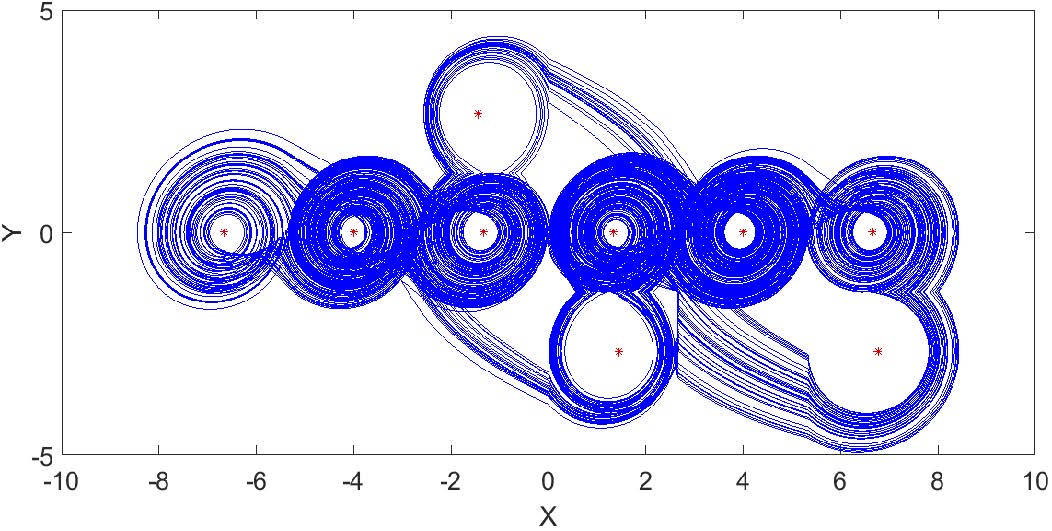
Fig. 2. Proyección del atractor dado por las ecs. (2) y (3) en el plano (𝑥, 𝑦) para la ley de conmutación de la ec. (4) con nueve atractores.
Mediante esta ley de conmutación se puede obtener un atractor de 9 enroscados, tal y como se muestra en la Fig. 2. Note que la posición de dichos enroscados desplazados en el espacio, corresponde a lo propuesto en el diagrama de la Fig. 1. Los puntos de equilibrios obtenidos tras resolver 𝑿∗ = −𝐀-𝟏𝐁 con los valores de la ec. (4) se muestran en la Tabla II.
Ahora mediante este sistema propuesto se diseñará la llave para el proceso de encriptación como se muestra a continuación.
C. Generador de bits pseudoaleatorio.
Este generador se basa en las series de tiempo obtenidas a partir de los estados caóticos del sistema de multienroscados dados por las ecuaciones.
La idea es calcular la solución del sistema mediante algún método iterativo, como el método de Runge Kutta de 4to orden, y evolucionar el sistema n veces para obtener una secuencia 𝑿 después de 1000 iteraciones del estado transitorio. Aprovechando la sensibilidad a las condiciones iniciales en sistemas caóticos, se considera que cada conjunto de ellas da como resultado diferentes series de tiempo. Por lo tanto, cada valor se puede considerar como una clave de cifrado, si se aumenta el número de enroscados, la dinámica del sistema es más compleja y la calidad del cifrado aumenta. A continuación, el generador de bits pseudoaleatorio (PRNG) se define similar a lo reportado en [1], de la siguiente manera:
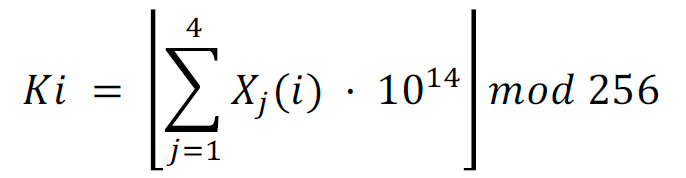
Aquí 𝜅𝑖 ∈ {0, 1, 2,…, 255} e 𝑖 = 1,…, 𝑛 , donde 𝑛 = 𝑙 × 𝑚 con 𝑙,𝑚 de acuerdo con el tamaño de la imagen en escala de grises a ser encriptado.
D. Diseño del esquema de cifrado y descifrado.
Después de crear las secuencias generadas por el sistema caótico con nueve atractores, encriptamos la imagen usando un cifrado de flujo similar a los descritos en [7,8]. El propósito de cifrar información con el PRBG propuesto es demostrar que las secuencias con diferente número de atractores generan una imagen de cifrado diferente, es decir, la calidad de encriptación mejora si se aumenta el número de atractores. El proceso para cifrar la imagen es píxel por píxel de la siguiente manera:
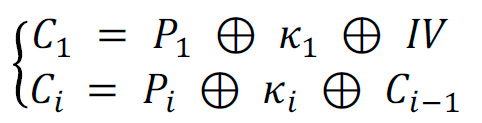
Donde 𝐶𝑖 y 𝑃𝑖 con 𝑖 = 2, . . . , 𝑛 son los pixeles de la imagen de cifrado y la imagen normal, respectivamente. Para mejorar la seguridad en el proceso, se considera una retroalimentación en el cifrado (Ci-1) y un vector inicial, donde IV ∈ {0, 1, . . . , 255} es un vector de inicialización (Initial Vector) usado una vez para el primer pixel, 𝜅𝑖 es la secuencia de bits pseudoaleatoria, el símbolo ⊕ es la operación XOR, que se ejecuta bit a bit en el bloque de 8 bits por píxel.
Para descifrar correctamente la imagen, el receptor debe tener la misma corriente de claves (formada por las condiciones iniciales X0, el vector de inicialización IV y la función de descifrado). Esta función toma la siguiente forma:
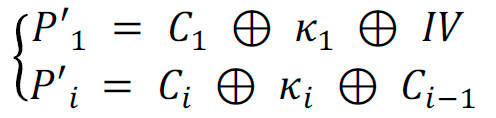
Si se usan la clave correcta 𝜅𝑖 y el vector de inicialización correcto IV, entonces la imagen original se obtendrá correctamente, es decir, 𝑃´𝑖 = 𝑃𝑖.
III. RESULTADOS
A. Cifrado de la imagen.
Para probar el método de cifrado y descifrado, se consideró la imagen en escala de grises de Lena de 256x256 pixeles, por lo que la Fig. 3 (a) muestra la imagen original; la imagen de cifrado se presenta en la Fig. 3 (b) y la imagen descifrada se muestra en la Fig.3 (c).
Para estudiar la seguridad y calidad del proceso de encripción se implementaron los análisis del histograma y el estudio de la correlación entre imágenes que se describen a continuación.
Fig. 3. Imagen Lena: (a) original; (b) cifrada; (c) descifrada.
B. Análisis de histogramas.
El histograma muestra cómo se distribuyen los píxeles en una imagen. Traza el número de píxeles según el nivel de escala de grises. Una propiedad que debería satisfacer un sistema de encriptación es que el histograma de la imagen encriptada presenta una distribución uniforme. Por lo tanto, los histogramas entre la imagen original y la imagen encriptada deben ser completamente diferentes. La Fig. 4 muestra el histograma de la imagen original y la Fig. 5 muestra el histograma de la imagen cifrada. Es importante mencionar que este último representa una distribución uniforme como se esperaba.
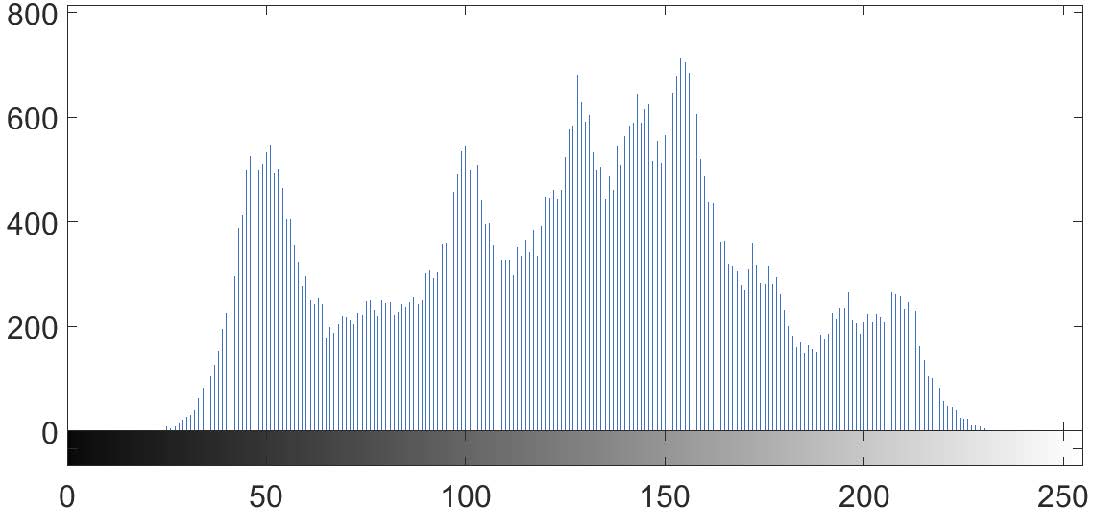
Fig. 4. Histograma de la imagen de Lena original.
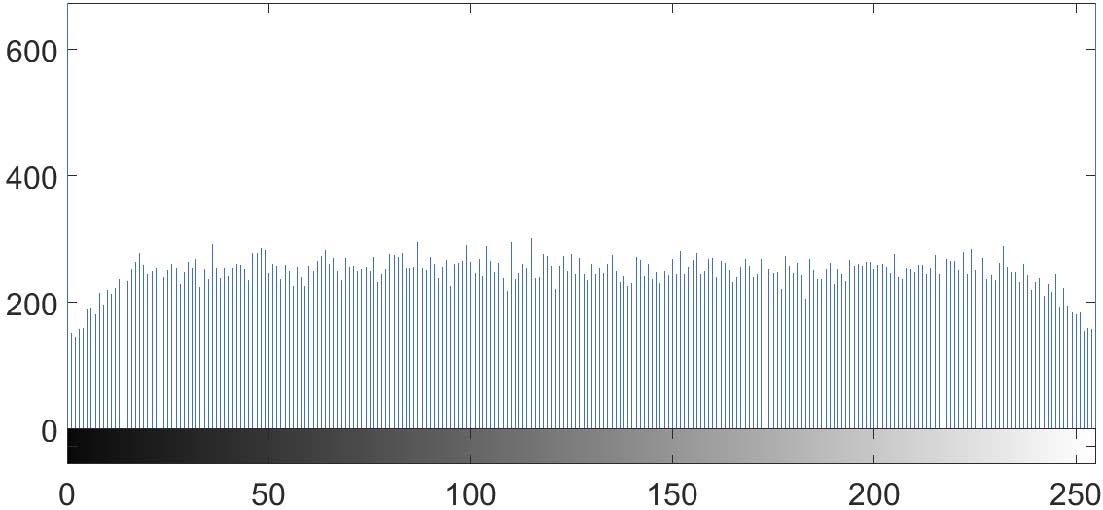
Fig. 5. Histograma de la imagen de Lena cifrada.
C. Análisis de correlación entre la imagen original y la encriptada.
Para mostrar que la imagen cifrada es independiente de la imagen simple, calculamos el coeficiente de correlación entre ambas imágenes. Si el coeficiente es cercano a 0, sugiere que no existe una correlación lineal o una correlación lineal débil. Los resultados para las imágenes en escala de grises se enumeran en Tabla II.
TABLA II. Coeficientes de correlación entre las imágenes simples y sus correspondientes imágenes cifradas.
| Imagen | descriCoeficientes de correlaciónpcion |
|---|---|
| Lena | 0.0010040 |
| Mandril | -0.0044883 |
| Pimientos | -0.0036057 |
Podemos observar que los coeficientes son cercanos a cero (incluso para dos imágenes más Mandril y Pimientos que no se incluyeron en el trabajo por cuestión de espacio), mostrando que las imágenes simples son independiente de las respectivas versiones cifradas [9].
IV. CONCLUSIONES
En este trabajo presentamos un estudio de los sistemas lineales por pedazos produciendo atractores caóticos de multiple enroscado tanto en el eje 𝑥 como el de 𝑦 mediante la ubicación de los puntos de equilibrio. Las trayectorias caóticas que este atractor genera debido a su alta sensibilidad a las condiciones iniciales, fue utilizado para generar un vector de números aleatorios para el diseño de una llave para la encriptación de imágenes en escala de grises. Se sometió el sistema a pruebas para verificar la seguridad del cifrado y determinar si es confiable como medio de cifrado de información, saliendo favorecido por los análisis del histograma y la correlación entre la imagen original y la imagen cifrada. A futuro se planea someter el sistema a más pruebas de criptoanálisis y de esta manera determinar su seguridad y eficacia, así como implementar el estudio de incluir más puntos de equilibrio y de generar más enroscados al atractor. Así como estimar el tiempo de latencia y costo computacional de este sistema de cifrado.
V. AGRADECIMIENTOS
L.J. Ontañón García Pimentel agradece el apoyo recibido por el Proyecto FAI-UASLP con número de registro C18-FAI-05-45.45. A la SEP-PRODEP por el apoyo otorgado en UASLPCA-268 con número de referencia IDCA 28234. Y al PFCE por el apoyo otorgado a la CARAO en el recurso P/PFCE 2018-24MSU0011E22.
VI. REFERENCIAS
- [1] H. Cheng, Partial encryption of compressed images and videos, IEEE Trans. Signal Process. 48 (8) (2000) 2439–2451.
- [2] N. Bourbakis, C. Alexopoulos, Picture data encryption using scan patterns, Pattern Recognit. 25 (6) (1992) 567–581.
- [3] S. Wijaya, S.K. Tan, S.U. Guan, Permutation and sampling with maximum length CA or pseudorandom number generation, Appl. Math. Comput. 185 (1) (2007) 312–321.
- [4] A.M.D. Rey, J.P. Mateus, G.R. Sánchez, A secret sharing scheme based on cellular automata, Appl. Math. Comput. 170 (2) (2005) 1356–1364.
- [5] M. García-Martinez, L. J. Ontañón-García, E. Campos-Cantón, S. Čelikovský, Hyperchaotic encryption based on multi-scroll piecewise linear systems, Applied Mathematics and Computation 270 (2015) 413-424.
- [6] Salgado Castorena, M. and Campos Cantón, E. (2016). Atractores caóticos con múltiple enroscado. Acapulco, Guerrero. 4° Encuentro de Jóvenes Investigadores – CONACYT. 11° Coloquio de Jóvenes Talentos en la Investigación.
- [7] Ontanon Garcia, L. J., Jiménez López, E., Campos Cantón, E., y Basin, M. (2014). A family of hyperchaotic multi-scroll attractors in Rn. Applied Mathematics and Computation, 233, 522-533.
- [8] H. Liu, X. Wang, A. Kadir, Color image encryption using choquet fuzzy integral and hyper chaotic system, Optik 124 (18) (2013) 3527–3533.
- [9] X. Wang, J. Zhao, Z. Zhang, Chaotic encryption algorithm based on alternant of stream cipher and block cipher, Nonlinear Dyn. 63 (4) (2011) 587–597.
- [10] M. T. Ramírez-Torres, J. S. Murguía, M. Mejía Carlos, Image encryption with an improved cryptosystem based on a matrix approach, International Journal of Modern Physics C Vol. 25, No. 10 (2014) 1450054.
- ISSN: 3061-8991
- Vol 1, 2025