CRIPTOANÁLISIS Y MEJORA A SISTEMA DE CIFRADO HIPERCAÓTICO PARA IMÁGENES
M. T. Ramírez-Torres1, C. A. Guerra García1, C. Montalvo2
1Coordinación Académica Región Altiplano Oeste, Universidad Autónoma de San Luis Potosí, San Luis Potosí, México,
tulio.torres@uaslp.mx, cesar.guerra@uaslp.mx
2Facultad de ingeniería Universidad Autónoma de San Luis Potosí, San Luis Potosí, México,
carlos.soubervielle@uaslp.mx
Abstract— En los últimos años, ha habido iniciativas para aplicar diferentes sistemas caóticos a la criptografía. En la propuesta mostrada por García-Martínez et al, los autores mostraron un nuevo sistema de cifrado basado en un PRBG (Pseudo Random Bit Generator), capaz de generar secuencias binarias utilizando los cuatro estados de un sistema hipercaótico multienroscado. Aun cuando esta propuesta se evaluó a través de seis pruebas de seguridad (análisis de espacio clave, entropía…etc.) este sistema presenta una debilidad, al momento de aplicar un ataque de imágenes en claro elegidas, conocido como Chosen Plain Image Attack (CPIA). En este trabajo se presenta un criptoanálisis al sistema y una propuesta de mejora.
Keywords—Criptoanálisis, vulnerabilidad, ataque.
I. INTRODUCCIÓN
En la actualidad, debido a la demanda de seguridad de la industria 4.0, por todos los procesos que requieren trabajar en línea, y el almacenamiento seguro de información confidencial, se han propuesto diversos algoritmos criptográficos con diferentes enfoques, destacando los de caótico. Esto debido a propiedades que tienen como, ergodicidad y la sensibilidad a condiciones iniciales. Sin embargo en muchas ocasiones estos nuevos sistemas presentan debilidades ante ataques de criptoanálisis y/o criptoanálisis diferencial. Provocando la fuga de información confidencial. Por ejemplo en [1], utilizan una secuencia pseudoaleatoria generada por un sistema hipercaótico para cifrar las imágenes, utilizando la operación XOR y la suma modular. Este sistema fue analizado en [2] y se encontraron debilidades al momento de aplicar el ataque CPIA. Por otra parte, en [3] se propuso un método de cifrado y de generación de cajas de sustitución basado en caos. Sin embargo en 2018, se publicó en [4], las debilidades del sistema propuesto por Çavuşoğlu et. al, bajo el ataque chosen-plaintext attack. En [5] los autores proponen un algoritmo de cifrado de imágenes caótico, basado en la entropía de la información. En el mismo año, Li et. al, en [6] revelan los problemas de seguridad que presenta dicho sistema ante ataques diferenciales. Por lo que podemos ver que es necesario un análisis mas profundo en diferentes escenarios, para poder validar un nuevo sistema de cifrado.
Para el cifrado de imágenes existen diversas consideraciones, debido a propiedades intrínsecas de éstas, como una gran tasa de datos y una alta correlación adyacente. Por lo tanto los algoritmos propuestos para estas áreas deben cumplir con dos tipos de seguridad: criptográfica y perceptual[7]. Algunos nuevos sistemas se enfocan solo en la seguridad perceptual y los autores validan sus resultados con pruebas estadísticas. Descuidando aspectos de seguridad ante otro tipo de ataques.
Por lo tanto, en este trabajo se busca ilustrar de manera explicita, una forma de llevar a cabo el ataque CPIA y una forma de mejorar el sistema de cifrado analizado. Buscando que futuros desarrolladores consideren estas pruebas y diseñen algoritmos de cifrado resistentes y eficientes. Este artículo se conforma de la siguiente manera, en la sección II se describe el sistema de cifrado propuesto por García-Martínez, mientras que en la sección III se detalla el proceso de criptoanálisis. En la sección IV se muestra la mejora que se propone y un breve análisis. Y en la sección V se encuentran las conclusiones.
II. SISTEMA DE CIFRADO
García-Martínez propuso un sistema de cifrado para imágenes en escala de grises en el trabajo [8]. Hace uso de un nuevo PRBG que produce secuencias binarias, utilizando cuatro estados de un sistema hipercaótico multienroscado.
Las imágenes son cifradas pixel a pixel utilizando las siguientes ecuaciones:
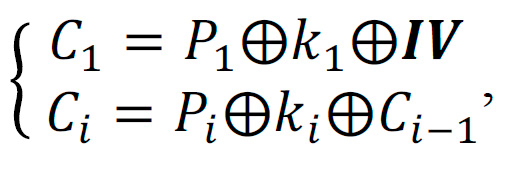
donde C y P representan los pixeles cifrados y en claro respectivamente, con 𝑖 = 2. . 𝑛. 𝑰𝑽 representa un vector inicial de 8 bits, 𝑘 es una secuencia aleatoria de 8 bits obtenida del PRBG. Y por último, el símbolo ⨁ representa la operación XOR. Para obtener el primer pixel cifrado 𝐶1, se calcula una operación XOR entre el coeficiente del pixel 𝑃1, la secuencia aleatoria 𝑘1 y el vector inicial 𝑰𝑽. Los siguientes pixeles cifrados 𝐶𝑖, se obtiene realizando una operación XOR entre el coeficiente del pixel 𝑃𝑖 , una nueva secuencia aleatoria 𝑘𝑖 y el pixel cifrado previo 𝐶𝑖=1 . Este proceso se repite hasta cifrar todos los pixeles de la imagen. Las condiciones iniciales del PRBG funcionan como llave secreta.
Como podemos observar el esquema cifra directamente los coeficientes de los pixeles, sin utilizar una operación de sustitución previamente, esto permite a los atacantes introducir datos de manera arbitraria.
III. CRIPTOANÁLISIS
En el ataque Chosen Plain Image Attack, el atacante es capaz de seleccionar las imágenes en claro y obtener sus respectivas versiones cifradas, sin embargo no posee la llave secreta. Este ataque fue aplicado al esquema de García-Martínez, como se describe en [9]. Para ilustrar este proceso, vease la Fig. 1. El ataque comienza seleccionando las dos imágenes en claro, en este caso se utiliza la imagen de Lena, Fig. 1a), y una imagen solida negra, Fig. 1b). Ciframos ambas imágenes con el algoritmo de García-Martínez con las mismas condiciones iniciales, y las imágenes que se obtienen son, Fig. 1c), Lena cifrada, y la Fig. 1d), la imagen solida cifrada, la cual llamaremos Mascara 𝑰0. Para recuperar la imagen de Lena sin conocer las condiciones inciales basta con calcular una operación XOR entre ambas imágenes cifradas, pixel a pixel. El resultado lo podemos ver en la Fig. 1e), que como se puede ver esta imagen revela patrones muy significativos de la Fig. 1a). Aun así el proceso de recuperación se puede mejorar, nuevamente sin conocer las condiciones iniciales y la imagen se puede recuperar al 100%, como se puede ver en la Fig. 1f). El proceso para obtener esta imagen será explicado más adelante.

Fig. 1. Chosen Plain Image Attack. a) Imagen de Lena, b)imagen solida negra, c)imagen de Lena encriptada, d)máscara, e) imagen recuperada con la operación XOR, f) imagen recuperada usando (3).
Este ataque funciona en este esquema, posiblemente por varias razones, pero este trabajo se enfoca en la falta de una función de sustitución, para evitar que el adversario introduzca valores en las ecuaciones a su conveniencia. Para ilustrar la debilidad observemos (2), esta ecuación representa el paso del ataque, donde se hace la operación XOR pixel a pixel.
Donde 𝐶L1 representa el primer pixel de la imagen de Lena cifrada, 𝐶M1 representa el primer pixel de la Mascara 𝑰M. Y por último, 𝑃L1 representa el primer pixel de la imagen de Lena. Como se puede ver, al momento de calcular la operación XOR entre ambos pixeles, los elementos de la ecuación de cifrado se reducen aplicando algebra booleana, y el resultado es el coeficiente 𝑃L1. Para recuperar los demás pixeles se utiliza (3), esta versión es la usada en la Fig. 1f). Para mejorar su desempeño en la recuperación, agregamos una operación XOR entre los pixeles cifrados previos, adicional a la de pixel a pixel, como se muestra a continuación:
como se puede ver, es posible recuperar la imagen original, sin conocer la llave secreta.
IV. MEJORA PROPUESTA
Para mejorar el sistema se propone agregar una función de preprocesamiento, capaz de sustituir el texto plano antes de ser cifrado. Sin importar que el texto en claro sea altamente redundante, esta función debe intercambiarlo por diferentes valores de la codificación, con igual probabilidad. Si se desea utilizar una caja de sustitución, el algoritmo debería modificarse, ya que simplemente intercambiar el texto con una S-box antes de cifrar, crearía patrones de la imagen original.
La función de preprocesamiento utilizada en esta mejora fue diseñada en [10]. Esta función se basa en la sincronización de autómatas celulares, usando la regla local 90. Es una modificación de un generador de números pseudoaleatorios propuesto en [11]. Gracias a su retroalimentación, la función de preprocesamiento puede intercambiar valores idénticos por números diferentes en cada iteración.
Para explicar su funcionamiento, en la Fig. 2 se ilustra el generador pseudoaleatorio y el proceso de evolución hacia atrás usando la regla 90. Se utiliza un vector 𝒙 y un vector 𝒚 de 𝑛 bits y 𝑛 + 1 bits, respectivamente. Se evoluciona hacia atrás, utilizando la operación XOR como indican las flechas, hasta generar el vector 𝒕. Esta función es llamada h.
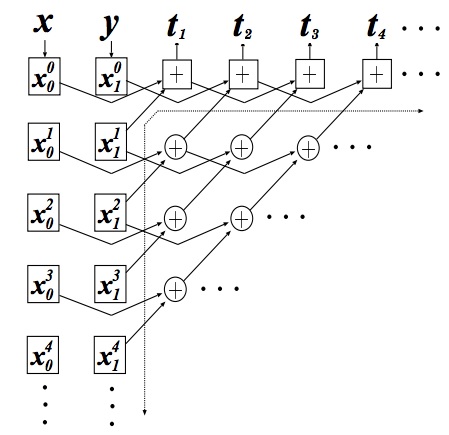
Fig. 2. Generador de secuencias pseudoaleatorias 𝒕 de 𝑛 bits, basado en la evolución hacia atrás de la regla 90.
Para aplicar esta operación como función de preprocesamiento, en la Fig. 3, podemos observar a la función ℎ como un bloque, y en el lugar del vector 𝒙, entra el coeficiente del pixel 𝒑, y en el lugar del vector 𝒚, un nuevo vector llamado 𝒛. Esto para diferenciar su funcionamiento como generador de números seudoaletorios y como función de preprocesamiento. El vector de salida es llamado ![]() , para señalar que es la versión procesada de 𝒑.
, para señalar que es la versión procesada de 𝒑.
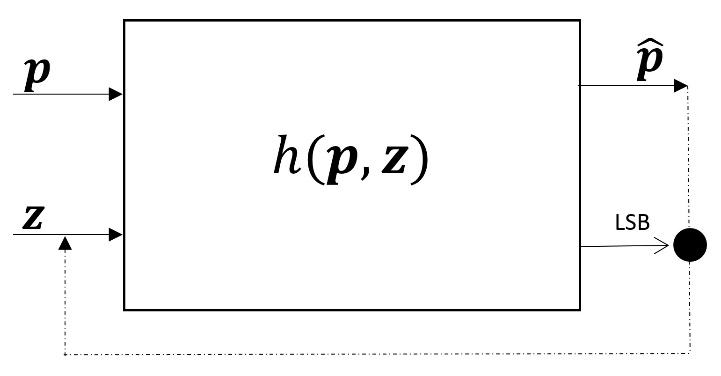
Fig. 3. Función de preprocesamiento. 𝒑 es el coeficiente del pixel, 𝒛 un vector aleatorio. A la salida se obtiene el vector preprocesado ![]() .
.
Como se puede ver existe una retroalimentación que actualiza el vector 𝒛, este nuevo vector se calcula con el vector de salida ![]() , concatenando el bit menos significativo del vector 𝒛, en la posición de bit más significativo.
, concatenando el bit menos significativo del vector 𝒛, en la posición de bit más significativo.
La diferencia entre esta función y una caja de sustitución la podemos observar en la Fig. 4.
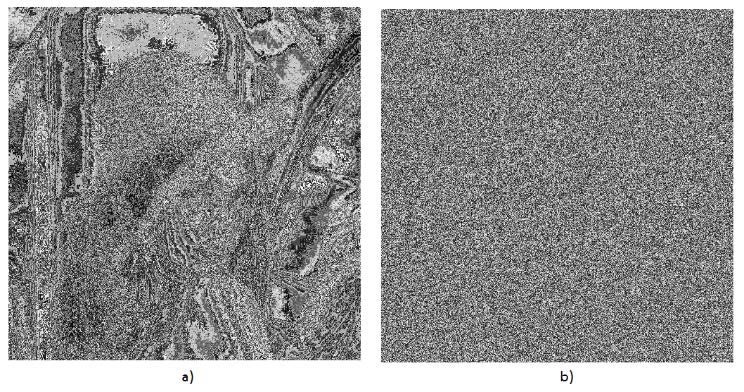
Fig. 4. a) imagen de Lena sustituida con una S-box del sistema AES (Advanced Encryption Standar), b) imagen de Lena despues de ser preprocesada con la función ℎ.
Se puede observar que en el caso de la caja se sustitución se crean patrones, debido a que no existe ningún tipo de dinámica, los coeficientes de la imagen son sustituidos siempre por los mismos valores de la S-box.
En la Fig. 5 se muestra el histograma de la imagen de Lena y su versión preprocesada. Como se puede ver el histograma se vuelve uniforme, ocultando la redundancia de la imagen original y previniendo un ataque estadístico.
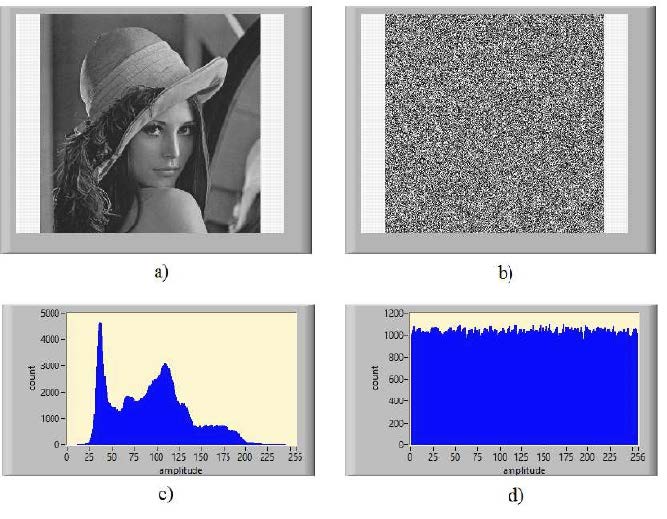
Fig. 5. Análisis de histogramas. a) Imagen de Lena, b)imagen preprocesada de Lena, c)histograma de a) y d)histograma de b).
Agregar la función de preprocesamiento al algoritmo de García-Martínez, antes del cifrado, mejora su desempeño ante el ataque CPIA. Lo anterior se puede confirmar en la Fig. 6, donde nuevamente se escogen las mismas dos imágenes de forma arbitraria.

Fig. 6. Chosen Plain Image Attack. a) Imagen de Lena, b)imagen solida negra, c)imagen de Lena encriptada, d)máscara, e) imagen recuperada con la operación XOR.
Como podemos observar el atacante no puede introducir el valor de 0 de forma arbitraria en las ecuaciones de cifrado, esto evita que capture información en la Mascara 𝑰0. Además la información no está cifrada de manera directa, el preprocesamiento intercambia los valores, por lo tanto ante condiciones que se dan en este ataque, no queda expuesta la información.
V. CONCLUSIONES
Los sistemas caóticos pueden aportar elementos en el diseño de sistemas de cifrado. Sin embargo, su análisis debe ser profundo e interpretar de manera general las pruebas que se aplican a los esquemas de cifrado. Ya que en algunos casos la fundamentación para realizar de cierta manera una prueba es porque se copia de otro trabajo, sin analizar los supuestos que considera el ataque y que las condiciones cambian en cada sistema de cifrado.
El cifrado de imágenes sigue presentado áreas de oportunidad y desarrollo, porque cuando un sistema logra solventar las problemáticas de seguridad incrementa su latencia. Por lo que la búsqueda de nuevos métodos se mantiene aún en auge y los sistemas caóticos pueden brindar soluciones a este problema.
REFERENCIAS
- [1] C. Zhu, “A novel image encryption scheme based on improvedhyperchaotic sequences” Optics communications, 2012, vol. 285, pp. 29-37, Jan. 2012.
- [2] C. Li, Y. Liu, T. Xie, M. Z Chen, ”Breaking a novel image encryption scheme based on improved hyperchaotic sequences” Nonlinear Dynamics, vol. 73, pp. 2083-2089, May 2013.
- [3] Ü. Çavuşoğlu, et al. “Secure image encryption algorithm design using a novel chaos based S-Box” Chaos, Solitons & Fractals, vol. 95, pp. 92-101, Feb. 2017.
- [4] C. Zhu, G. Wang, K. Sun, “Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos based S-box” Symmetry, vol. 10, pp. 399. Sept. 2018.
- [5] G. Ye, C. Pan, X. Huang, Z. Zhao, and J. He, ‘‘A chaotic image encryption algorithm based on information entropy’’ Int. J. Bifurcation Chaos, vol. 28, 2018.
- [6] C. Li, et al. “Cryptanalysis of a chaotic image encryption algorithm based on information entropy” IEEE Access, vol. 6, pp. 75834-75842, 2018.
- [7] S. Lian, Multimedia content encryption: techniques and applications, Auerbach Publications, 2008.
- [8] M. García-Martínez, L. J. Ontañón-García, E. Campos-Cantón, & S. Čelikovský, “Hyperchaotic encryption based on multi-scroll piecewise linear systems” Applied Mathematics and Computation, vol. 270, pp. 413-424, Nov. 2015.
- [9] S. Li, C. Li, G. Chen, & K. T. Lo, “Cryptanalysis of the RCES/RSES image encryption scheme.” Journal of Systems and Software, vol. 81, pp. 1130-1143, Jul. 2008.
- [10] M. T. Ramírez-Torres, J. S. Murguia, M. Carlos Mejía, “Image encryption with an improved cryptosystem based on a matrix approach.” International Journal of Modern Physics C, vol. 25, pp. 1450054, Apr. 2014.
- [11] J. Urias, E. Ugalde, G. Salazar, “A cryptosystem based on cellular automata,” Chaos, vol. 8, pp. 819-822, Dec. 1998.
- ISSN: 3061-8991
- Vol 1, 2025