Actas de Ciberseguridad para la Industria 5.0

EN BÚSQUEDA DE POLINOMIOS PRIMITIVOS PARA GENERACIÓN DE SECUENCIAS MEDIANTE LFSR

Alejandro Padrón-Godínez¹, Rafael Prieto Meléndez², Victor Emmanuel Hernández López³

¹Inst. y Medición, ICAT - Coord. Óptica UNAM – INAOE CDMX - Tonantzintla, Puebla - México,
apadron@inaoep.mx

²2Instrumentación y Medición, ICAT UNAM CDMX, México,
rafael.prieto@ccadet.unam.mx

³Lab. Optica Facultad de Ciencias – UNAM Cto. Escolar S/N, CDMX - México,
carlost@inaoep.mx

Resumen— En la solución de algoritmos eficientes en la generación de secuencias binarias mediante LFSR en cifradores de flujo se emplean polinomios primitivos para obtener los periodos máximos, que dependen del número de bits utilizados además de una semilla de bits diferente de cero. Algoritmos que tienen una complejidad polinomial en su solución, es decir el tiempo que tardan en correr y que crecen con el número de bits n en la entrada son de manera polinomial nx con Z en una programación clásica. En el presente trabajo mostramos una búsqueda de polinomios primitivos para la obtención de los periodos máximos mediante un algoritmo clásico, la implementación en dispositivos de lógica programable en VHDL de un LFSR para la verificación de los periodos máximos y resultados preliminares en la solución del algoritmo mediante simulaciones en cómputo cuántico en la generación de secuencias binarias pseudoaleatorias.

Palabras Clave—Cifradores de Flujo, Sistemas de Lógica Programable FPGA, Polinomios Primitivos.

I. INTRODUCCIÓN

La generación de secuencias binarias pseudoaleatorias generadas por sistemas de cómputo digitales han permitido que muchas aplicaciones tanto en software como en hardware puedan emplearse en algoritmos estándares de Criptografía. El manejo de la información clasificada o privada en forma segura es tan necesaria como la utilización de dispositivos modernos y actualizados. La velocidad de las comunicaciones en diversas transacciones nos anuncia el empleo de cifradores de flujo casi en tiempo real, ésta es la necesidad para que los algoritmos de cifrado deban ser optimizados ante los nuevos desarrollos tecnológicos y puedan evitarse ataques a los sistemas de información. Ya han sido anunciados y publicados los algoritmos poscuánticos que tratan de evitar que sean ciptoanalizados justamente ante el poder de cómputo con plataformas cuánticas. [1]. En el ámbito de la implementación usando algoritmos de cifrado por flujo se han podido crear algunas estructuras mediante registros lineales retroalimentados por desplazamiento “LFSR” (Linear Feedback Shift Register, por sus siglas en inglés), como Shrinking, Geffe, Beth - Piper, sincronizadas o no por mencionar algunas. Esto para disminuir la posibilidad de alterar, modificar, borrar información que pueda ser interceptada por personal no autorizado (Hacker) aunque siempre habrá intentos mal intencionados. Algunos de los primeros algoritmos de flujo ya han sido quebrantados,

PASPA-DGAPA-UNAM beca de doctorado.

por los mismos desarrolladores o grupos de criptoanalistas para mostrar sus vulnerabilidades ante la nueva tecnología computacional, ejemplo de ellos son RC4, A5 1 y WPA. Aunque estos algoritmo han sido y fueron las raices para los nuevos algoritmos que en combinación con modos de operación y otros algoritmos inclusive de bloque que aumentan el nivel de seguridad como en el caso de WPA2 y WPA3 con claves de AES-256.

Los LFSR se han utilizado para aplicaciones en comunicaciones celulares GSM, aunque para estas implementaciones no se rigen por un estándar ya que estos algoritmos se han mostrado en cuestiones de enseñanza para generación de secuencias binarias mediante operaciones OR-exclusivas. Lo que inicialmente se necesita una estructura que debe consistir de número de bits, semilla o vector de inicio VI (diferente de cero) y polinomio primitivo para su funcionamiento. [2], Fig. (1).

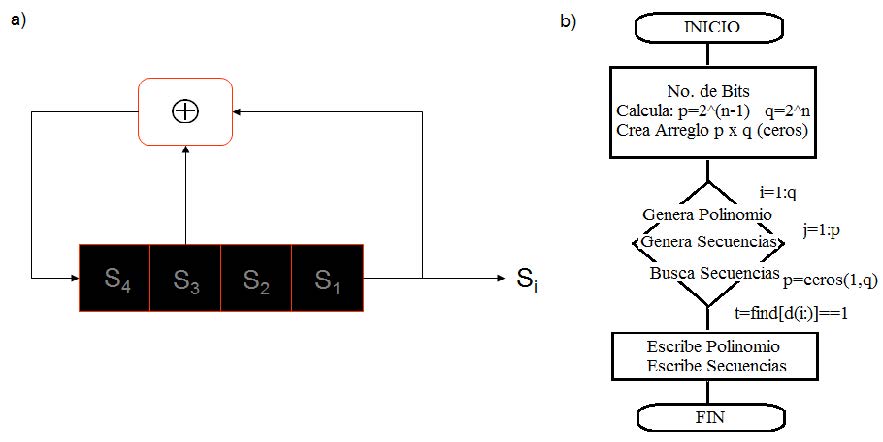
Figura 1. a) Diagrama de un LFSR de 4 bits con P(x) = x³ + x + 1 y b) diagrama de flujo para el cálculo del polinomio primitivo y secuencias generadas.

La seguridad de los cifradores de flujo empleando polinomios primitivos de mayor orden aumenta, debido a que el periodo de las secuencias binarias obtenidas es mayor. Como se sabe el periodo máximo es el producto de cada periodo máximo empleado en el diseño de una configuración en particular. El diseño de nuevas configuraciones mediante LFSR, empleando polinomios primitivos, pueden ser más eficientes comparados con cifradores de flujo empleando modos de operación y cifradores de bloque. Lo cual puede analizarse en el tiempo de procesamiento de los criptogramas obtenidos, por ejemplo un cifrador de bloque convertido en cifrador de flujo tiene que calcular las subclaves en cada iteración, en particular un “Output Feedback Block” con un AES-128.

En cuestiones de seguridad de la información se debe estar al tanto de que si se comprometen las claves secretas se compromete toda la seguridad de los sistemas protegidos. Por tal motivo hay que tomar en cuenta que la generación de claves, la distribución y el almacenamiento debe de efectuarse de forma segura. Sin embargo, el papel de contar con algoritmos de cifrado actualizados es primordial para proteger estos sistemas de información. Los algoritmos criptográficos modernos tendrán sus vulnerabilidades y podrán explotarse en cuanto se tenga acceso a plataformas modernas. Se podrá intentar criptoanalizar estos algoritmos, ya que con el uso de cómputo cuántico se trata de optimizar los algoritos clásicos para que procesen en menor tiempo. Un atacante que conoce el algoritmo puede intentar romper su seguridad y posiblemente tendrá a las manos las herramientas modernas, al mismo tiempo que se estén desarrollando los algoritmos postcuánticos. [3], [4].

Así empleando generadores de secuencias binarias pseudoaleatorios a partir de registros de desplazamiento retroalimentados lineales (LFSR por sus siglas en ingles) [5], se plantea la búsqueda de los polinomios primitivos de acuerdo al número de bits empleados, mediante un programa que prueba la combinación de polinomios hasta que se obtenga el periodo máximo. La razón de esta búsqueda de polinomios primitivos se debe a que en la literatura sólo se menciona que existen tablas donde se pueden encontrar estos generadores de secuencias y que no son de fácil acceso. Se pueden verificar si con los polinomios primitivos se obtienen los periodos máximos realizando las pruebas estadísticas publicadas por la NIST en la norma SP 800-22 para generadores secuencias pseudoaleatorias en aplicaciones criptográficas o simplemente usando los Postulados de Golomb incluidas como pruebas en la misma norma. En paralelo se desarrolla una implementación de un LFSR en Lenguaje de Descripción de Hardware (VHDL) sobre Sistemas de Logica Programable (FPGA) bajo la plataforma de desarrollo Xilinx, mostrando los resultados en una simulación para un número de bits, una semilla y de acuerdo al polinomio primitivo seleccionado.

En este trabajo también se muestra un desarrollo preliminar bajo la plataforma de Qiskit para bajo un modelo cuántico como puede generarse dada la densidad de probabilidad una secuencia binaria pseudoaleatoria en cada proceso. Planteando con esto si es posible implementar el algoritmo desarrollado para encontrar los polinomios primitivos de acuerdo al número de bits empleados para optimizar su cálculo. En las conclusiones mostraremos la problemática que se encontró cuando el número de bits aumenta y se mostrarán las perspectivas del trabajo. [6].

II. CARACTERÍSTICAS DE LOS LFSR

Los LFSR han sido planteados como generadores de claves por varias razones, por ejemplo: son fáciles de implementar en hardware, producen secuencias con periodo grandes, producen secuencias binarias con buenas propiedades estadísticas y debido a su estructura pueden ser analizados con técnicas algebraicas [7]. Cuando se usan LFSR, la seguridad de los sistemas de comunicación depende mucho de que tan vulnerable sea el medio de transmisión y como puede verse afectado ante ataques pasivos y activos. En implementaciones reales como GSM, se encuentran algunas propiedades que deben cumplir dentro un sistema de seguridad de información para su buen funcionamiento:

a) El cifrado debe poder ser integrado en la línea de comunicación sin tener que modificar el equipo de comunicaciones.
b) Debe manejar un flujo de información full-duplex asincrónica serial, soportando las diferentes velocidades de transmisión que son de uso general.
c) Debe permitir cambiar el número de bits a la entrada de una manera simple.
d) El proceso de cifrado/descifrado se debe hacer continuamente y en tiempo real.

Si se quiere alcanzar la primer propiedad, los algoritmos dentro del sistema de información deben de ser diseñados para imlementarse en cada lado del sistema de comunicación, se pueden colocar en los extremos de la línea de la transmisión, o se colocan como una interfaz entre el usuario y el equipo de comunicación. Dependiendo del uso en donde el cifrado será utilizado y de las características del equipo y del medio de transmisión será el lugar más conveniente para implementar el proceso de cifrado. El proceso de los LFSR dependen de tres parámetros principales, polinomio generador, número de bits y semilla de acuerdo con el número de bits. La Figura (2) muestra como pueden ser los polinomios de los generadores de secuencias binarias. Estos polinomios pueden ser factorizables,

Figura 2. Polinomios para el diseño de LFSR que dictan las operaciones sobre los registros de desplazamiento por retroalimentación.

irreducible y primitivos, para los cuales se buscan los polinomios primitivos que pueden generar el periodo máximo de acuerdo al número de bits empleados. Donde el periodo máximo se calcula como T_max = 2ⁿ−1, con n: No. de bits. La Figura (3) representa el diagrama de un LFSR para 8 bits. En el caso de que se utilicen polinomios que no son primitivos el periodo máximo no se alcanzará, la Figura(4) es un ejemplo de esto, para este LFSR de 4 bits se empleo una semilla “0111” y un polinomio generador P(x) = x⁴ + x² + 1. Como se verán en los resultados sólo existen dos polinomios primitivos generadores del periodo máximo para 4 bits.

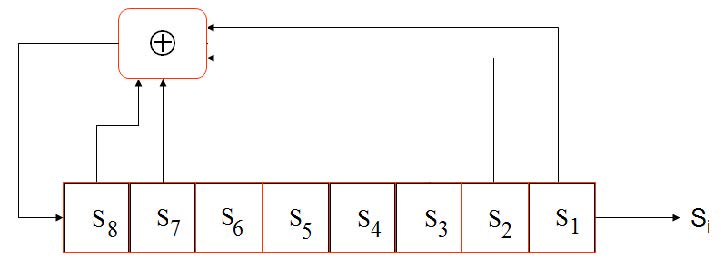
Figura 3. LFSR de 8 bits con operaciones xor para la retroalimentación según el polinomio primitivo P(x) = x⁸ + x⁷ + x² + x + 1.

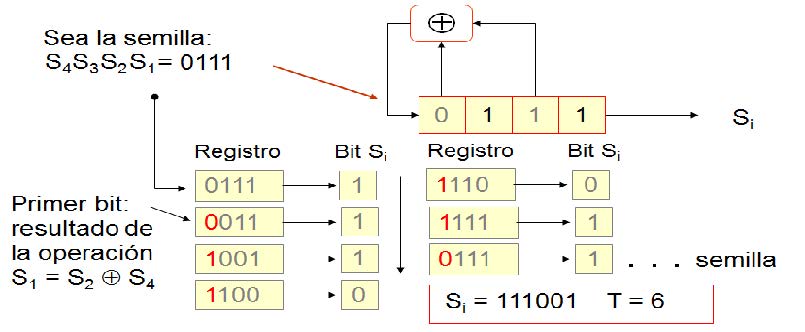
Figura 4. Polinomio que no genera las secuencias binarias del periodo máximo de un LFSR de 4 bits.

III. ESTRUCTURAS DE LFSR NO LINEALES

En la creación de estructuras no lineales usando LFSR se han construido varias estructuras donde se intenta aumentar el periodo de las secuencias binarias generadas, donde ahora el cálculo del periodo máximo es el producto del periodo máximo de cada LFSR contenido en la estructura. En la literatura se pueden encontrar algunas estructuras haciendo uso de LFSR en diferentes configuraciones que pueden ser síncronas o no sincronizadas. En la Figura(5) se muestra una primer distribución de LFSR conocida como generador Geffe. Una segunda estructura usando LFSR de diferentes tamaños se

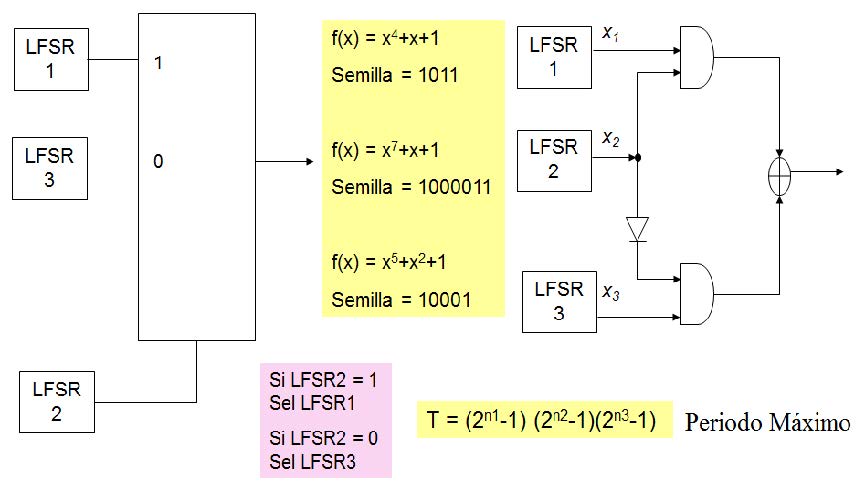
Figura 5. Diseño de un Generador Geffe de secuencias binarias.

ilustra en la Figura (6), denomida como generador Beth - Piper. Una tercer estructura al final de esta sección se presenta en la la Figura (7), que tiene el nombre de generador Shrinking. Hay muchos desarrollos de cifradores de flujo con diversas estructuras usando e implementando LFSR en su construcción que fueron las raices de las primeras aplicaciones como urnas electrónicas, tokens para control de acceso o en telefonía célula

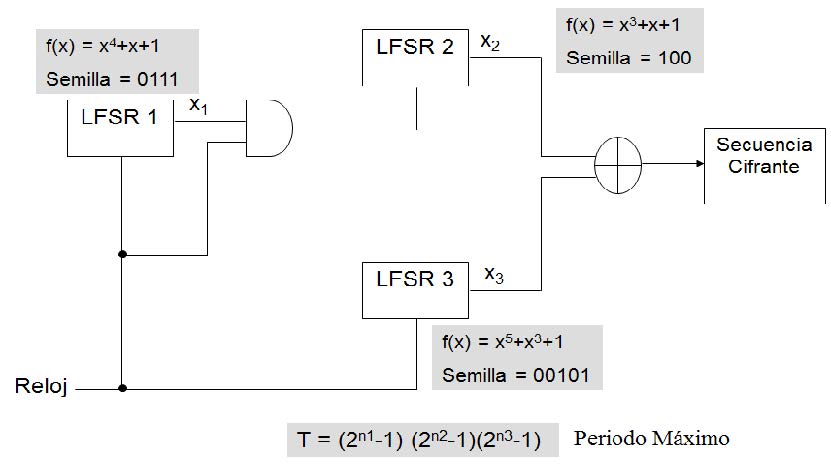
Figura 6. Estructura para un Generador Beth - Piper.

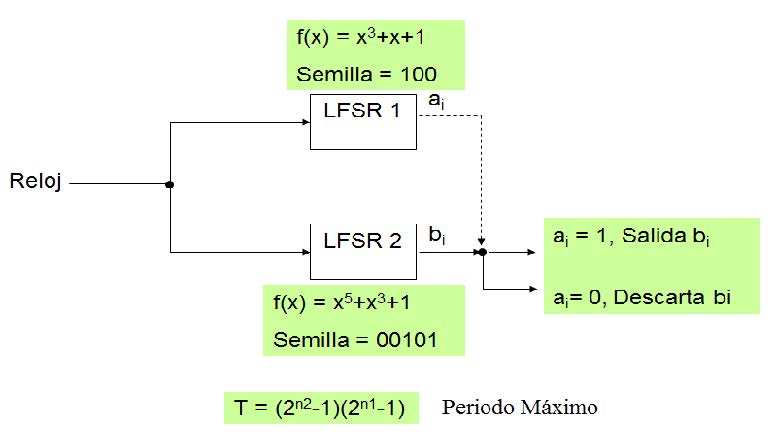
Figura 7. Configuración de un Generador Shrinking.

por mencionar algunas. Otras implementaciones contienen elementos adicionales como en el caso de los algoritmos A5 1 y A5 2 que emplean funciones de mayoría para variar los avances en cada paso de los LFSR en el proceso de envío de datos para cifrar y descifrar.

IV. ALGORITMO DE GROVER MODELO DE COMPUTACIÓN CUÁNTICO

Para la computación cuántica el algoritmo de Grover es uno de los algoritmos de búsqueda, que permite realizarla en un espacio de O(n^1/2) en ves de O(xⁿ) como los hacen los algoritmos clásicos. Este algoritmo permite realizar la búsqueda, mediante una densidad de probabilidad muy grande, un elemento de una secuencia no ordenada de una serie combinacional. El algoritmo de Grover tiene como meta encontrar un estado marcado (|t⟩) en un conjunto desordenado, mostrado por un elemento en la base canónica. Emplea como estado inicial la superposición uniforme de todos los elementos O(xⁿ) de la base computacional al que llamaremos |s⟩. El algoritmo se basa en aplicar sucesivamente el operador O = (2|t⟩⟨t| − I_d) y el operador G = (2|s⟩⟨s| − I_d). El operador O ó G tiene como vector propio al vector |t⟩ ó |s⟩ asociado al valor propio 1. El resto de los vlores propios son −1 y corresponden a una base de vectores ortogonales a |t⟩ ó |s⟩. Por lo tanto el operador de Grover U_g = G.O no es más que una reflexión sobre el subespacio generado por |t⟩ y |s⟩. Luego de aplicar O(n^1/2) iteraciones se obtiene un estado muy cercano a |t⟩. El algoritmo de Grover consiste de la iteración de las dos fases siguientes:

Consulta
Inversión sobre la media

Suponiendo que tenemos una lista de N componentes, en la que hay m elementos marcados, el algoritmo de Grover permite maximizar las amplitudes de los elementos marcados en un tiempo breve, lo que hace más fácil obtener un elemento marcado cuando se realiza la observación del sistema.

V. RESULTADOS PARA EL CÁCULO DE NÚMERO DE POLINOMIO PRIMITIVOS

En esta sección se muestran los resultados obtenidos para la búsqueda de los polinomios primitivos generadores de los periodos máximos en LFSR de acuerdo al número de bits de entrada. Para lograr este objetivo se desarrollo un programa computacional que prueba las diferentes combinatorias por número de bits que dieran como resultado precisamente el periodo máximo. En el programa también se tuvo el cuidado de obtener el tiempo de proceso cuando el número de bis empieza a aumentar. En la Tabla (I) se presentan los resultados hasta 14 bits debido a que la capacidad para guardar las secuencias generadas se ve limitada al espacio de almacenamiento generando archivos de Megabytes y el tiempo de espera va creciendo exponencilmente con el aumento de bits en la entrada. Motivo suficiente para optimizar este desarrollo para que sea eficiente y de ser posible implementarlo mediante plataformas de cómputo cuántico.

Cuadro I NO. POLINOMIOS GENERADORES DEL PERIODO MÁXIMO

No. de Bits	No. Pol. Prim.	Tiempo [s]
3	2	0.024378
4	2	0.009135
5	6	0.029094
6	6	0.098124
7	18	0.374736
8	16	1.482539
9	48	6.514709
10	60	23.359722
11	176	95.106123
12	144	384.922147
13	630	1558.68514
14	756	6392.023456

La Figura (8) muestra la gráfica de los resultados obtenidos, observándose que para valores mayores de bits en la entrada la tendencia en el tiempo es aumentar exponencialmente.

Analizando los resultados de la Tabla (I) y la Figura (8) se puede notar que el crecimiento en el número de polonomios generadores del periodo máximo no es contino o uniforme, en algunos casos aumenta y en un valor siguiente de bits en la entrada disminuye. Como en el caso entre 6, 7 y 8 bits de entrada y en 10, 11 y 12. En el caso de la columna del tiempo en la Tabla (I), estos valores siempre aumentan, ya que aunque el programa no se detiene hasta que prueba todas las posibles combinaciones 2n de polinomios generadores.

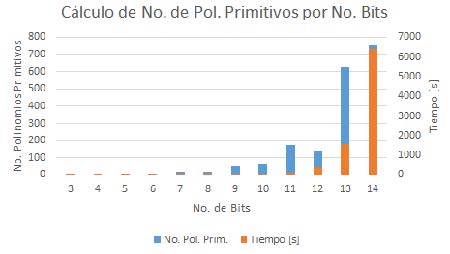
Figura 8. Resultados del cálculo de los Polinomios Primitivos por número de Bits y tiempo de procesamiento, datos de la Tabla (1).

Ahora se presentan los resultados para la implementación de un LFSR de 8 bits tomando el Polinomio Primitivo del renglón 98, que corresponde a P(x) = x8 +x7 +x2 +x+1. Polinomios Primitivos de 8 bits: (Iniciando con la potencia x1 con el bit menos significativo )

que corresponde al renglón 15 = [ 0 0 0 1 1 1 0 1 ]
que corresponde al renglón 22 = [ 0 0 1 0 1 0 1 1 ]
que corresponde al renglón 23 = [ 0 0 1 0 1 1 0 1 ]
que corresponde al renglón 39 = [ 0 1 0 0 1 1 0 1 ]
que corresponde al renglón 48 = [ 0 1 0 1 1 1 1 1 ]
que corresponde al renglón 50 = [ 0 1 1 0 0 0 1 1 ]
que corresponde al renglón 51 = [ 0 1 1 0 0 1 0 1 ]
que corresponde al renglón 53 = [ 0 1 1 0 1 0 0 1 ]
que corresponde al renglón 57 = [ 0 1 1 1 0 0 0 1 ]
que corresponde al renglón 68 = [ 1 0 0 0 0 1 1 1 ]
que corresponde al renglón 71 = [ 1 0 0 0 1 1 0 1 ]
que corresponde al renglón 85 = [ 1 0 1 0 1 0 0 1 ]
que corresponde al renglón 98 = [ 1 1 0 0 0 0 1 1 ]
que corresponde al renglón 104 = [ 1 1 0 0 1 1 1 1 ]
que corresponde al renglón 116 = [ 1 1 1 0 0 1 1 1 ]
que corresponde al renglón 123 = [ 1 1 1 1 0 1 0 1 ]
— No. de polinomios primitivos calculados:16 —

La Figura (9) muestra la simulación en VHDL del LFSR de 8 bits que se seleccionó, donde se uso una semilla inicial igual a “10000001” en amarillo como vector de inicio. En la misma figura se muestran los primeros 10 periodos en gris o iteraciones del LFSR y los periodos donde se repite la semilla, no en 255 sino en 256 por la carga de la semilla en el inicio de los periodos, cuando el reset en verde se coloca en 1.

La secuencia binaria generada es:

Secuencia:( 1 0 0 0 0 0 0 0 1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 1 1 0 0 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 1 0 1 1 0 0 0 0 1 0 1 0 1 1 0 0 1 0 0 1 1 1 0 0 1 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 0 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 0 1 1 1 0 0 0 1 0 1 1 1 0 1 0 0 1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 0 0 1 1 1 1 1 1 ).

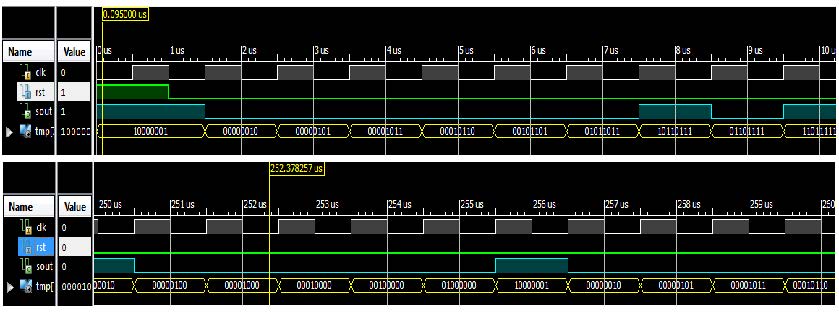
Figura 9. Simulación en ciclos de tiempo del LFSR de 8 bits seleccionado desarrollado en el simulador de la plataforma Xilinx.

Para este Polinomio Primitivo de grado ocho en particular se tienen los siguientes resultados cuando se realizan las pruebas estadísticas sobre la secuencia binaria generada [7].

Tamaño de la secuencia = 255
No. de ceros = 127
No. de unos = 128
La diferencia debe ser uno, 1er postulado,
Que también es 1/2 de la secuencia para PG2a
Dif.0sy1s = 1
****Prueba de frecuencia****
X1 = 0.0039
****Prueba de series o prueba de los 2-bit****
Longitud 2 = 63 64 63 64
Un 1/4 de la secuencia para PG2b
X2 = 0.0118
****Prueba de póquer ****
constantes m=3, k=85
Longitud 3 = 31 32 31 32 31 32 32 32
Que es 1/8 del tamaño de la secuencia para el PG2c
X3 = 668.2235
****Prueba de rachas****
NoBloques Tam123 = 32 16 8, NoHuecos Tam123 = 32 16 8
ValoresD e = 32.1250 16.0000 7.968 para calcular X4
X4 = 0.0012
****Prueba de Autocorrelación con XOR y desplazamiento****
X5 = -3.3883
Para el 3er Postulado de Golomb
Donde Xi son indicadores de las 5 pruebas
— Pruebas Estadísticas sobre la Secuencia Binaria —

Por último se presentan los resultados preliminares para optimizar el algoritmo utilizado con el cálculo de ceros y unos de un LFSR de 8 bits. La implementación práctica es de la siguiente manera, suponga que se tiene una función f tal que f(x) = 1 para los elementos marcados (conocidos). Se puede implementar un oráculo mediante un operador cuántico con ayuda de un qubit auxiliar. Si x es un estado cuántico de cualquier número de qubits y y el estado de un único qubit, se define a U_f |x⟩⊕|y⟩ = |x⟩⊕|y⟩⊕f(x), donde ⊕ representa la operación XOR de dos bits. Si se usa |y⟩ = |−⟩ = H|1⟩, se obtiene que U_f |x⟩|−⟩ = (−1)^f(x)|x⟩|−⟩, donde se nota que f(x) = 1 y se obtiene el cambio de signo en el estado |x⟩. Se observa que en ningún momento se necesitó conocer explícitamente f para implementar U_f , y en general, esta función depende del problema en cuestión. Para la implementación práctica como la compuerta U_f depende fuertemente de la función f, y esta a su vez depende del problema en cuestión. Así se debe construir de manera que se adapte a los elementos marcados o conocidos. Para un ejemplo donde la lista de búsqueda es de 2ⁿ − 1 = 255 elementos con n = 8, de los cuales 16 elementos son marcados. Se necesitan un bit auxiliar por lo que se necesitarán 9 qubits. La implementación del operador U_f en kisquit se haría como:

def Uf(circuito, qreg)
circuito.ccx(qreg[0],qreg[1],qreg[2].qreg[3],qreg[4],
qreg[5].qreg[6],qreg[7],qreg[8])

Es decir, el tercer qubit es controlado por los dos primeros, pero ocurre un efecto interesante, como los dos primeros qubits se les aplica la compuerta H al aplicar el operador CNOT los qubits de control se ven afectados, en particular el elemento correspondiente al índice |11111111⟩ sufre un cambio de signo, que es justo lo se busca, este fenómeno se conoce como phase kickback. Luego se implementa la inversión y se emplea la compuerta de Hadamard de 8X8 con entradas iguales a 0.5 y de -0.5 en la diagonal principal. Ahora se usan ambos operadores para implementar el algoritmo:

Se crea un circuito con 9 qubits, donde 8 serán los que representan la lista y el último es el qubit auxiliar
Se crea también 9 bits normales para almacenar las mediciones
Se aplica H a los ocho primeros qubits para ponerlos en superposición
Se lleva el qubit auxiliar al estado |−⟩ para aplicar U_f
Se aplica las fases de consulta e inversión las veces necesarias
Se devuelve el qubit auxiliar a su estado inicial
Se miden los resultados

En la Figura (10) se puede apreciar el circuito generado bajo la plataforma kisquit, en un inicio se observan 10000 veces el estado “11000011” el cual es el más observado al ejecutarlo una sola vez cada fase, que corresponde al elemento 98 seleccinado de la lista, que es el elemento marcado. Se puede

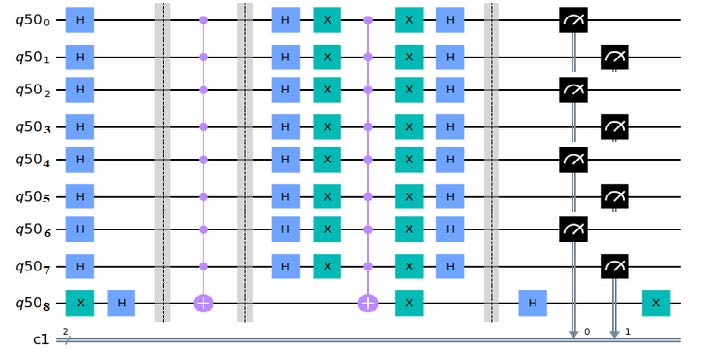
Figura 10. Modelo de Grover para 8 bits desarrollado en la plataforma cuántica Qiskit.

cambiar el número de iteraciones, por ejemplo dos iteraciones:

renglón 15 = [ 0 0 0 1 1 1 0 1 ] 624 observado
renglón 22 = [ 0 0 1 0 1 0 1 1 ] 626 observado
renglón 23 = [ 0 0 1 0 1 1 0 1 ] 620 observado
renglón 39 = [ 0 1 0 0 1 1 0 1 ] 622 observado
renglón 48 = [ 0 1 0 1 1 1 1 1 ] 631 observado
renglón 50 = [ 0 1 1 0 0 0 1 1 ] 627 observado
renglón 51 = [ 0 1 1 0 0 1 0 1 ] 619 observado
renglón 53 = [ 0 1 1 0 1 0 0 1 ] 617 observado
renglón 57 = [ 0 1 1 1 0 0 0 1 ] 627 observado
renglón 68 = [ 1 0 0 0 0 1 1 1 ] 621 observado
renglón 71 = [ 1 0 0 0 1 1 0 1 ] 605 observado
renglón 85 = [ 1 0 1 0 1 0 0 1 ] 629 observado
renglón 98 = [ 1 1 0 0 0 0 1 1 ] 645 observado
renglón 104 = [ 1 1 0 0 1 1 1 1 ] 633 observado
renglón 116 = [ 1 1 1 0 0 1 1 1 ] 623 observado
renglón 123 = [ 1 1 1 1 0 1 0 1 ] 630 observado
— No. de polinomios primitivos observados:16 —

Y así pueden seguirse calculando a través de más iteraciones, un detalle observado es que de acuerdo a las iteraciones en que se observa más el elemnto marcado son periódicas.

VI. CONCLUSIONES

Los resultados muestran el número de polinomios primitivos generadores de secuencias binarias para el periodo máximo, de acuerdo al número de bits a la entrada de cada LFSR. Así como el tiempo que se tardo en obtener los polinomios, en realidad las potencias para cada polinomio primitivo. Se mostró la gráfica de los resultados para ver la tendencia exponencial cuando aumenta el número de bits a la entrada. Como se mencionó antes de la Tabla (I), el algoritmo de búsqueda debe optmizar tal vez hasta 2^n/2 para reducir el espacio de almacenamiento y el tiempo para el cálculo, como en el caso del ataque por cumpleaños. Se presentó la simulación en VHDL para la verificación del periodo máximo en el caso particular de 8 bits en la entrada. Se hicieron pruebas estadísticas sobre las secuencias binarias producidas para este caso que se presentan en la literatura, desarrollando el programa para los Postulados de Golomb y las cinco pruebas de la referencia [7] para obtener los resultados mostrados. Se realizó las pruebas preliminares bajo la plataforma kisquit del modelo de Grover para encontrar secuencias binarias de ocho bits, en búsqueda de la optimización del algoritmo de búsqueda para encontrar las potencias de los polinimios primitivos aqui mostrados hasta 14 bits. Dado que el modelo de Grover realiza una búsqueda de un elemento en una secuencia no ordenada de 2ⁿ en un espacio de O(n^1/2). Sin dejar de mencionar, que el archivo para los resultados de 14 bits en la entrada pesa 64,414 Kbytes.

AGRADECIMIENTOS

Este trabajo ha sido financiado por la Dirección General de Personal Académico de la Universidad Nacional Autónoma de México bajo el Programa de Apoyos para la Superación del Personal Académico a través de la beca doctoral. En particular, un agradecimiento al Grupo Académico de Modelado y Simulación de Procesos del ICAT-UNAM, por el tiempo proporcionado en su equipo de 12 núcleos para el procesamiento de los cálculos en este trabajo presentados.

REFERENCIAS

[1] Daltabuit E., Hernández L., Mallén G., Vázquez J., “La seguridad de la Información,” Ed. Limusa, 2007.
[2] Prieto Meléndez R.,Padrón Godinez A., Herrera Becerra A.A., Calva Olmos V.G. Generic Platform for the Implementation of Stream Ciphers in FPGAs. 2nd ICIAS International Congress on Instrumentation and Applied Sciences, (2011).
[3] Martínez Reyes I., Padrón Godinez A., Prieto Meléndez R. Herrera Becerra A,A,. Calva Olmos V.G. Generador de números pseudoaleatorios usando AES con modo contador: implementación en FPGA. SOMI XXIX Congreso de Instrumentación, (2014).
[4] Padrón Godinez A., Información cifrada en medios portadores, Tesis de Maestría, ESIME-IPN (2013).
[5] Vázquez Sánchez J.A., Padrón Godinez A., Prieto Meléndez R. Herrera Becerra A,A,. Calva Olmos V.G. Cifrador de flujo para tecnología GSM: una comparación entre hardware y software. SOMI XXIX Congreso de Instrumentación, (2014).
[6] Prieto Meléndez R., Padrón Godinez A., Herrera Becerra A,A,. Calva Olmos V.G. Implantación Electrónica de Cifradores de Flujo Tipo Vernam Utilizando Generadores Pseudoaleatorios. SOMI XXVII Congreso de Instrumentación, (2012).
[7] Meneses J., Oorschot P., “Handbook of Applied Cryptography,” Ed. CRC Press Inc., 1997.

ISSN: 3061-8991
Vol 1, 2025