CAJAS S: UNA VISIÓN GENERAL ACERCA DEL CORAZÓN DE LOS CIFRADORES
David Carcaño Ventura1, Lil María Rodríguez Henríquez1,2, Saúl E. Pomares Hernández1,3
1Coordinación de Ciencias Computacionales, Instituto Nacional De Astrofísica Óptica y Electrónica, Puebla, Mexico,
carvendavid@gmail.com
2Consejo Nacional de Humanidades, Ciencias y Tecnologías Mexico City, Mexico
lmrodriguez@inaoep.mx
3CNRS, LAAS Toulouse, France
spomares@inaoep.mx
Abstract—Las cajas S son consideradas el corazón de los cifradores de llave simétrica debido a la no-linealidad que ofrecen. Estas cajas S son funciones booleanas con un trasfondo matemático complejo, lo que en ocasiones dificulta la comprensión de los conceptos, convirtiendo en un desafío profundizar en el tema. Por ello, este trabajo presenta una visión general sobre lo que es una caja S, explicando sus métricas de seguridad y mostrando el trabajo que actualmente está en desarrollo. De esta manera, este artículo pretende crear una motivación al lector para que se continúe explorando este tema.
Index Terms—Cajas S, Cifradores, AES, Ataque Diferencial, Propiedades de la Caja S.
I. INTRODUCCIÓN
Las cajas S son funciones booleanas que se han estudiado por más de 30 años debido a la seguridad que pueden ofrecer en los cifradores de llave simétrica. Éstas, consideradas como el corazón de los cifradores, son el principal componente para proveer el servicio de confidencialidad en la transmisión de datos [1], [2].
La caja S del cifrador AES 1 (siglas de Advanced Encryption Standard) [3] es una de las más utlizadas y estudiadas por la resistencia que ofrece ante los ataques criptográficos. Sin embargo, es suceptible a los ataques algebraicos debido a su construcción [4], y no siempre es la mejor opción para los cifradores ligeros [1]. Por lo que, en la actualidad se siguen buscando cajas S que puedan lograr un alto nivel de seguridad, utilizando un enfoque diferente de construcción y/o usando menos recursos de los dispositivos.
La búsqueda de nuevas cajas S es un desafío debido al inmenso espacio de búsqueda que existe y al complejo transfondo matemático. Por esta razón, se presenta una visión general sobre estas funciones de manera amigable, con el objetivo de que este trabajo sirva como referencia para introducir al novedoso tema sobre las cajas S.
El artículo se organiza de la siguiente manera. En la sección II se muestra como funciona un cifrador de llave simétrica y el secreto para lograr la seguridad en las comunicaciones. La sección III define y explica la definición formal de la caja S. La sección IV presenta las diferentes representaciones de la caja S. En la sección V, se expone como obtener el nivel de seguridad de una caja S y se ejemplifica el caso del ataque diferencial. La sección VI muestra el trabajo actual sobre las cajas S. Y por último, la seccion VII presenta la conclusión de este trabajo.
II. EL SECRETO DE LA SEGURIDAD EN LAS COMUNICACIONES
Los cifradores son una primitiva criptográfica usada para transmitir información confidencial entre dos o más entidades (personas, computadoras, robots, etc.). La figura 1 muestra como Alicia le envia un mensaje cifrado a Bob a través de un canal inseguro de comunicación. A pesar de que el adversario puede interceptar el mensaje cifrado Msj_C, éste no podrá conocer el mensaje original.
Para lograr esto, ambas entidades necesitan una llave sk. Ésta es secreta y solo las entidades de confianza deben tenerla (en este caso Alicia y Bob). Con esta llave, Alicia cifra el mensaje original Msj (también conocido como texto en claro) usando el cifrador C, y obtiene un mensaje cifrado Msj_C. Bob recibe Msj_C y recupera el mensaje original Msj usando la inversa del cifrador C−1 (también conocido como descifrador) y la llave sk.
Como se ha mencionado, el adversario puede interceptar el mensaje cifrado, ya que el canal de comunicación es inseguro. Sin embargo, el adversario no podrá descifrar el mensaje ya que no tiene la llave secreta. Además, aunque el adversario use un ataque de fuerza bruta, podría tomarle decadas encontrar la llave secreta [5].
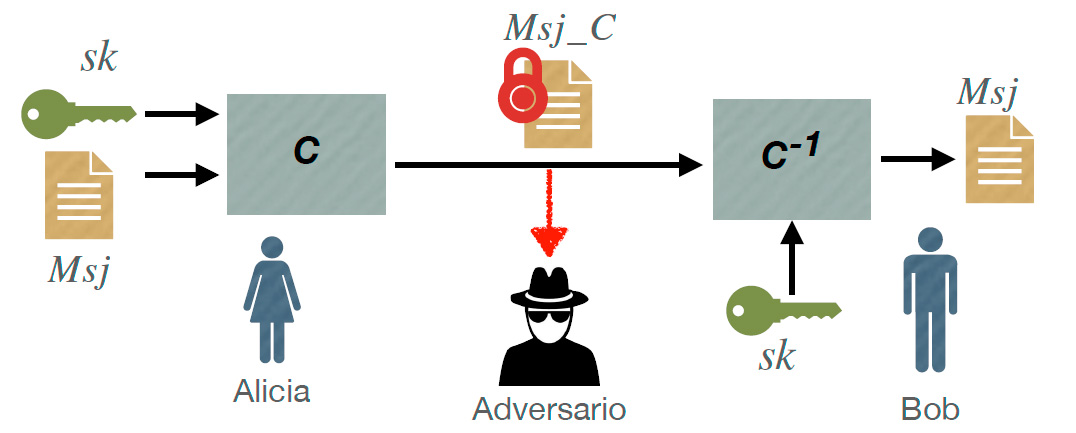
Fig. 1. Transmisión segura de datos entre Alice y Bob usando el cifrador C y la llave secreta sk.
A. Confusión y Difusión
Shannon estableció que un cifrador debe de cumplir con dos principios llamados confusión y difusión para garantizar la confidencialidad en el envío de información [6]. El principio de confusión establece que se debe romper la relación de la llave secreta con el texto cifrado. Mientras que el principio de difusión propone que se debe romper la estrucura estadística del texto en claro. Es decir, que si un bit del texto en claro cambia, al menos la mitad de los bits del texto cifrado también deben cambiar
Estos principios rompen las relaciones entre el texto en claro y el texto cifrado, así como entre la llave secreta y el texto cifrado, de tal forma que el adversario no pueda encontrar patrones para romper la seguridad del cifrador
Diferentes cifradores como AES [3], TWINE [7], ASCON [8] y CLEFIA [9] son usados para brindar seguridad en las comunicaciones. Para ofrecer los principios mencionados, estos cifradores utilizan cajas S (cajas de sustitución).
Las cajas S son funciones no lineales que actúan como los componentes principales en los cifradores, generando textos cifrados incomprensibles para el adversario. En la figura 2, se puede observar este efecto al cifrar el texto en claro Msj_Secreto = 128 utilizando AES-128 y la llave secreta 0123456789abcdef. Por esta razón, las cajas S son consideradas como el corazón de los cifradores.
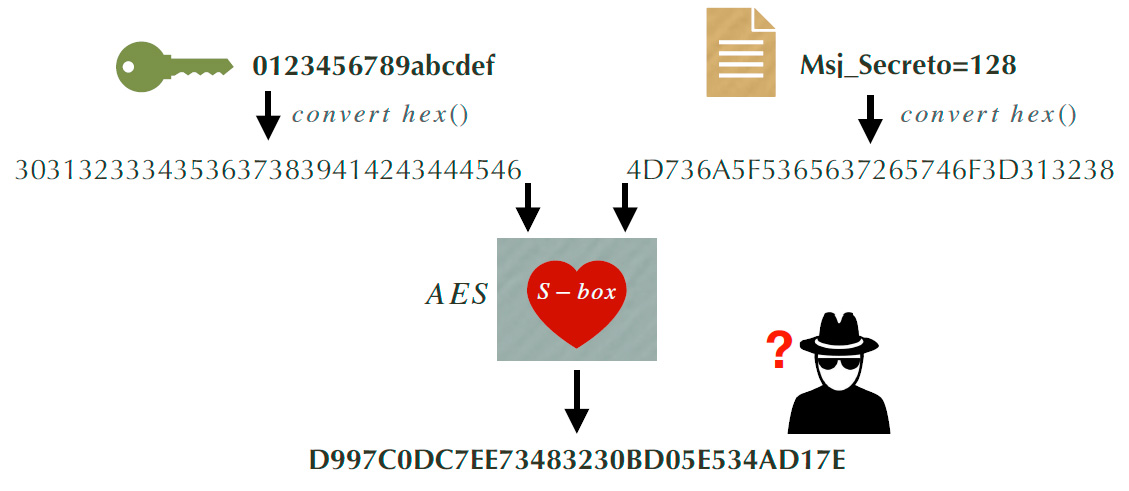
Fig. 2. Funcionamiento del cifrador AES.
III. .QUÉ ES UNA CAJA S?
La caja S de un cifrador sustituye los bits del estado del cifrador. Esta caja recibe n bits de entrada y devuelve m bits de salida. Una definición más formal se presenta en [2], y es la siguiente:
Definición 1: Una caja S de tamaño n × m es una función booleana vectorial que sustituye un vector de dimensión n a un vector de dimensión m y se denota de la siguiente manera: S :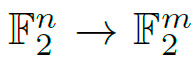 
, donde n,m son enteros positivos y 
es un vector de dimensión n en el espacio 
.
Daemen y Rijmen, los creadores de AES, diseñaron una caja S de tamaño n = m = 8 con el enfoque de construcción algebraico usando la función inversa X−1, donde X representa los 8 bits de entrada. Esta caja se puede ver de la siguiente manera:
Debido a la seguridad que puede ofrecer, esta caja S sirve como referencia para el diseño de nuevas funciones no lineales. Esta función, que utiliza operaciones con polinomios, es el elemento clave más importante del cifrador AES. Dado que este cifrador es uno de los más utilizados, su caja S se ha convertido en el secreto para garantizar la seguridad de las comunicaciones [2], [3].
IV. REPRESENTACIONES DE LA CAJA S
Las representaciones de la caja S ayudan a la visualización de este componente, así como su implementación en software y hardware, y permiten conocer el nivel de seguridad de la misma. En esta sección hablaremos de dos: LUT (siglas de Look Up Table) y ANF (siglas de Algebraic Normal Form).
Por conveniencia de espacio, ejemplificaremos estas representaciones con la caja del cifrador TWINE. Esta caja emplea la misma construcción que AES (enfoque algebraico con la función inversa), pero usa un tamaño menor el cual es n = m = 4. Sin embargo, el lector se puede referir a [10] donde Bao et al. muestran la LUT y la ANF de la caja S de AES usando su herramienta PEIGEN [2].
A. Look Up Table (LUT)
Esta representación muestra todos valores de entrada y su respectiva salida en una tabla (o matriz). Las dos primeras columnas de la tabla I muestra la LUT de la caja de TWINE. Existen diversas ventajas al emplear esta representación, entre las cuales se destacan las siguientes:
- Visualización: La LUT de una caja S permite visualizar los valores de entrada y sus correspondientes sustitutos (valores de salida), sin necesidad de realizar los cálculos de la función.
- Implementación: Cuando se implementa una caja en software, se utiliza la LUT de la caja para crear una matriz y almacenar los datos en memoria. De esta manera, cuando el cifrador necesita la caja, no emplea recursos en computar este componente, si no que solo busca los valores correspondientes en la matriz y los sutituye en el estado del cifrador [1].
- Nivel de seguridad de la caja: La LUT permite analizar la caja S para conocer su resistencia ante ataques criptográficos como los diferenciales.
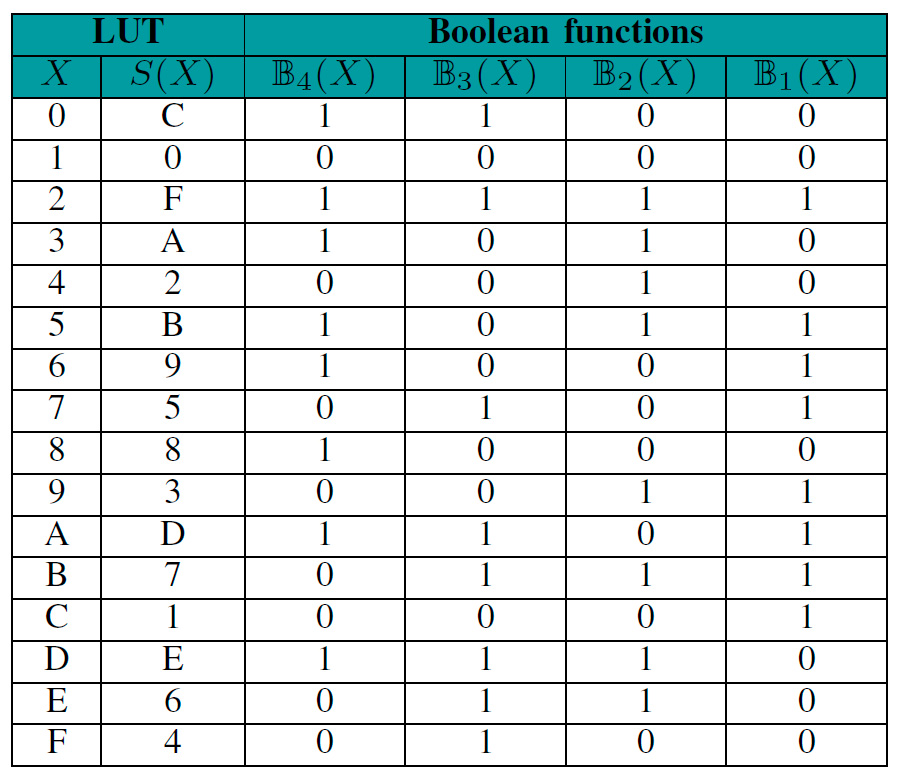
TABLA I LUT DE LA CAJA S DE TWINE Y SUS FUNCIONES BOOLEANAS
B. Algebraic Normal Form (ANF)
Las cajas S de tamaño n × m son funciones booleanas vectoriales. Sin embargo, estas cajas pueden ser la unión de m funciones booleanas. Por tanto, se presenta la siguiente definición:
Definición 2: Una función Booleana relaciona un vector de dimensión n a un elemento que pertenece a . En otras palabras la función lleva al vector de dimensión n a 1 o 0, y se denota de la siguiente manera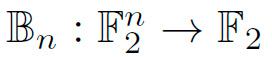 
La tabla I muestra la LUT de la función vectorial de la caja de TWINE y sus 4 funciones Booleanas. Se puede observar que la unión de las cuatro funciones Bi(X) es la representación binaria de la salida hexadecimal S(X). Esta conversión ayudará a enteneder la representación ANF de una caja S.
La ANF es una forma de representar cada función booleana de la caja S como el producto y sumatoria de sus entradas. Es decir, si tenemos m salidas, entonces tendremos m representaciones ANF de la caja, las cuales se llamaran coordenadas.
Las siguientes funciones Booleanas representan la ANF de las coordenadas de la caja de TWINE, donde X representa los cuatro bits de entrada X = {x3, x2, x1, x0}:
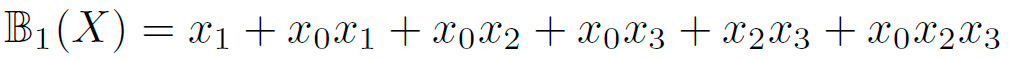
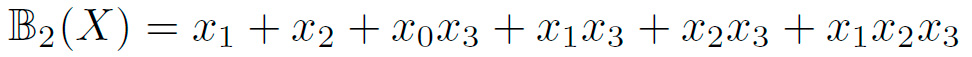
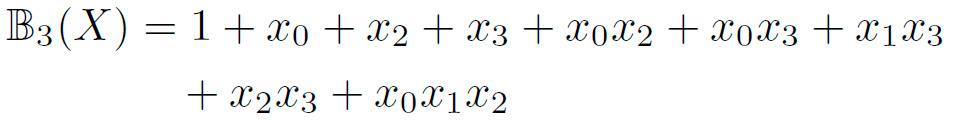
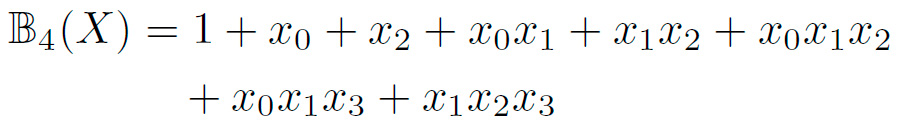
Es posible notar que en la tabla I, X representa los 4 bits de entrada de la caja. Por lo que si calculamos cada una de las funciones (1),(2),(3), y (4), usando los bits de entrada, podremos encontrar las salidas de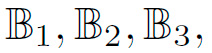 
y 
respectivamente.
Las ventajas de esta representación son:
- Visualización: Observar la forma algebraica de la caja S.
- Implementación: Las implementaciones de la caja S en hardware requieren calcular la función cada vez que el cifrador lo necesite, con el objetivo de no ocupar la memoria del dispositivo. Usando la ANF de la caja se pueden crear operaciones tipo Bit-slice para computar la salida de la caja cada vez que el cifrador lo requiera [11], [12].
- Nivel de seguridad de la caja: Usando esta representación, se puede evaluar el nivel de seguridad de la caja ante ataques algebraicos.
Existen otro tipo de representaciones como la polar, pero las representaciones LUT y ANF son las más utilizadas en el estudio de cajas S.
V. NIVEL DE SEGURIDAD DE LA CAJA S
Al ser la caja S el corazón de los cifradores, ésta se ha convertido en el primer objetivo de los adversarios para vulnerar el cifrador usando los ataques shrortcut [13]. Estos ataques son más agresivos que los de fuerza bruta, ya que pueden reducir el trabajo computacional considerablemente para encontrar la llave secreta del cifrador.
Estos ataques se componen de dos fases:
- El adversario intenta obtener distintivos analizando la caja S y encontrando patrones. Un distintivo es una característica que lleva información sobre la llave cuando es procesada por las rondas de un cifrador [14], [15].
- Usando los distintivos obtenidos en la fase anterior, junto con parejas de textos en claros, y sus correspondientes textos cifrados, el adversario puede recuperar algunos o todos los bits de la llave secreta.
La caja S es fundamental para que el adversario no encuentre distintivos en el cifrador. Por ello, esta función debe ser lo más segura posible, pero .cómo podemos medir la seguridad de la caja?. La caja S tiene propiedades que permiten saber la resistencia ante ataques criptográficos. Estas propiedades ayudan a adversarios y diseñadores. Si los valores de las propiedades están alejados de lo óptimo, entonces el adversario puede vulnerar la caja para encontrar distintivos. En el mismo caso, pero para el diseñador, estos valores le permiten incrementar el nivel de seguridad del cifrador mediante el diseño de otra caja, para mejorar estos defectos y presentar una función más resistente.
La tabla II muestra algunos ataques y las propiedades a las que están relacionadas. En esta tabla se puede observar que un solo ataque puede estar asociada a muchas propiedades. Así pues, si se desea que una caja sea resistente a un ataque, el diseñador debería tomar en cuenta todas las propiedades relacionadas a ese ataque. Lograr lo óptimo en una sola propiedad no muestra la resistencia completa al ataque.
TABLA II RELACIÓN DE LOS ATAQUES CRIPTOGRÁFICOS CON LAS PROPIEDADES DE LA CAJA S. LAS DEFINICIONES FORMALES DE ESTAS PROPIEDADES PUEDEN SER ENCONTRADAS EN DIFERENTES ARTÍCULOS INCLUYENDO [2], [16]–[18].
| Ataque | Propiedad |
|---|---|
| Diferencial | Uniformidad diferencial (DU) Balance (B) CarD1 |
Lineal
Algebraico |
Linealidad (L) CarL1 No-linealidad |
| Grado algebraico (AD) Minimo grado algebraico (MAE) Inmunidad algebraica (IA) Inmunidad algebraica de un grafo (GAI) |
A continuación, se explicará el funcionamiento general de los ataques diferenciales y como podemos obtener una propiedad relacionada a este tipo de ataque, conocida como uniformidad diferencial.
A. Resistencia de la caja S a los ataques diferenciales
La figura 3 muestra como se realiza un ataque diferencial a un cifrador C en tres pasos. En el primer paso, se observa como el adversario elige un texto en claro P1 y dos constantes a, b. Luego crea un segundo texto en claro P2 computando la operación P1 ⊕ a. P1, P2 son dos textos en plano con una diferencia a. En el segundo paso, el adversario cifra los dos textos en plano P1, P2 y obtiene C1,C2 respectivamente. En el tercer paso, el adversario compara la diferencia de C1⊕C2 con respecto a la constante b. Si la comparación es correcta, entonces el adversario empieza a encontrar patrones para crear los distintivos. El objetivo de los ataques diferenciales es encontrar patrones cuando se analizan diferencias de textos en claro y sus respectivas salidas.
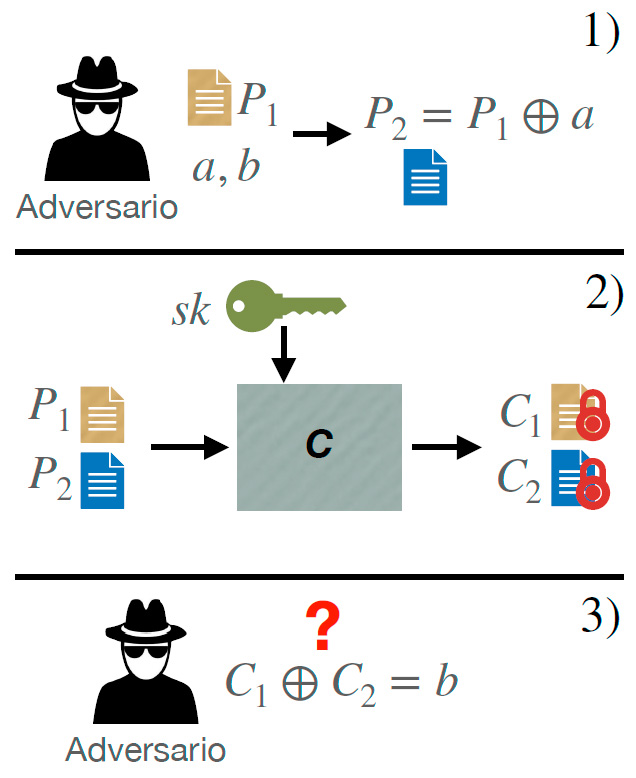
Fig. 3. Ataque diferencial a un cifrador C.
El ataque diferencial es uno de los más poderesos debido a que:
- Puede reducir el factor de trabajo para encontrar la llave secreta. En [15], Stamp y Low muestran como se puede reducir el factor de trabajo a la mitad, en comparación a los de fuerza bruta, para encontrar la llave secreta del cifrador FEAL.
- En [19], Shamir y Biham demuestran cómo encontrar distintivos diferenciales en todas las rondas del cifrador DES, a pesar de que sus cajas S presentan una alta resistencia frente a este tipo de ataque.
- En la literatura, el diseño de cifradores que usan este tipo de función no lineal (tipo esponja [8], de flujo [20], caóticos [21], de bloque [14]) contemplan el ataque diferencial para evaluar la seguridad del cifrador y de la caja S.
Tomando como base el trabajo de Shamir y Biham en [19], a pesar de que el cifrador presente las cajas S con la más alta resistencia ante los ataques criptográficos, aún puede ser vulnerado. Sin embargo, esto debe de servir como motivación para seguir buscando cajas S que alcancen siempre el mejor nivel de seguridad, ya que si éstas presentan una vulnerabilidad, recuperar la llave será más sencillo.
En la literatura, el diseño de cajas S contemplan diversas propiedades relacionadas a este tipo de ataque entre ellas uniformidad diferencial, balance y CarD1. Este trabajo explica la uniformidad diferencial [22] que se obtiene usando una herramienta llamada DDT (siglas de Distribution Differential Table) [23]. Esta herramienta usa la LUT de la caja y se define de la siguiente manera:
Definición 3: DDT: Sea una caja S y dos vectores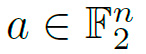 
and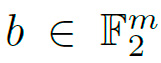 
, la DDT de S es una tabla de tamaño 2n × 2m donde cada celda contiene el número de parejas a, b que cumplen la siguiente ecuación:
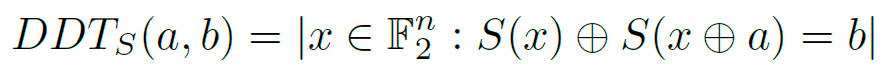
Cada celda de esta tabla refleja el número de veces que se cumple la ecuación (2) cuando se le da un valor a los vectores a y b. Se debe contemplar que x representa todos los datos de entrada de la caja S. En otras palabras, si consideramos x = 8 con la LUT de la caja S de TWINE, y elegimos los valores de a = 5 = 0101 y b = 6 = 1010 tendremos que verificar la siguiente igualdad:
S(1000) ⊕ S(1000 ⊕ 0101) = 0110
1000 ⊕ S(1101) = 0110
1000 ⊕ 1110 = 0110
0110 = 0110
6 = 6
Se puede notar que al resolver la ecuación, se cumple la igualdad. Si la ecuación se cumple, entonces el contador de DDT(a, b) (la celda de este ejemplo DDT(5, 6)) incrementa en uno. Ahora, si se quiere obtener el número de ecuaciones que cumplen la igualdad (2) cuando a = 5 y b = 6, se necesita resolver todas las ecuaciones cuando x toma el valor de todas las entradas de la caja S. Sin embargo, ya existen programas
TABLA III DDT DE LA CAJA DE TWINE.
DDT |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
0 |
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
2 |
2 |
4 |
0 |
0 |
2 |
2 |
0 |
0 |
0 |
2 |
2 |
2 |
0 |
2 |
0 |
0 |
4 |
2 |
0 |
0 |
2 |
0 |
3 |
0 |
0 |
2 |
0 |
0 |
2 |
2 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
4 |
4 |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
0 |
0 |
2 |
0 |
4 |
0 |
2 |
2 |
2 |
5 |
0 |
2 |
4 |
2 |
0 |
0 |
2 |
2 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
2 |
0 |
0 |
0 |
4 |
0 |
2 |
0 |
2 |
0 |
0 |
2 |
2 |
2 |
0 |
7 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
0 |
2 |
4 |
0 |
0 |
2 |
0 |
0 |
0 |
8 |
0 |
2 |
2 |
4 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
2 |
9 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
4 |
0 |
2 |
0 |
2 |
2 |
0 |
2 |
A |
0 |
2 |
0 |
0 |
2 |
0 |
0 |
4 |
2 |
2 |
0 |
2 |
0 |
0 |
0 |
2 |
B |
0 |
0 |
2 |
0 |
2 |
0 |
2 |
2 |
0 |
0 |
0 |
2 |
2 |
4 |
0 |
0 |
C |
0 |
0 |
2 |
0 |
2 |
0 |
0 |
0 |
2 |
2 |
2 |
0 |
0 |
2 |
4 |
0 |
D |
0 |
4 |
2 |
2 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
2 |
0 |
2 |
0 |
E |
0 |
2 |
0 |
0 |
4 |
0 |
2 |
0 |
0 |
0 |
2 |
0 |
2 |
0 |
2 |
2 |
F |
0 |
2 |
0 |
0 |
0 |
2 |
4 |
0 |
2 |
0 |
2 |
2 |
0 |
2 |
0 |
0 |
como PEIGEN [2] o SAGE [24], los cuales evaluan la caja y presentan el valor de todas las celdas de DDT. La tabla III muestra la DDT de la caja de TWINE.
Si las celdas de la DDT presentan valores altos, significa que la caja es más propensa a mostrar características diferenciales. En otras palabras, se puede vulnerar la caja para encontrar los distitivos de la primer fase del ataque. Por lo tanto, se presenta la siguiente definición:
Definición 4: DU (siglas de distribution uniformity): Es el valor más grande de la DDT donde a ̸= 0 y se denota como:
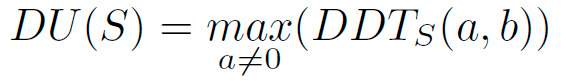
Este valor debe ser lo más pequeño posible para que las cajas presenten la mayor seguridad ante este tipo de ataques. El DU que logra la caja de TWINE es 4 y es el valor más pequeño que se puede lograr cuando n = 4 (en otras palabras se considera el valor óptimo en ese caso).
VI. TRABAJO A DESARROLLAR SOBRE LAS CAJAS S
El objetivo principal de este tema es la búsqueda de nuevas funciones con alta resistencia a los ataques criptográficos. Sin embargo, ésto se divide en diversas líneas de investigación; aquí presentaremos tres: los compromisos entre las propiedades, las cajas S para cifradores ligeros y los enfoques de construcción
A. Compromisos entre las propiedades
La búsqueda de nuevas cajas S implica considerar que existen conflictos entre las mismas propiedades; al lograr lo óptimo en una, se puede alterar el nivel de seguridad de otra. En consecuencia, el diseñador debe establecer compromisos para lograr un equilibrio en el nivel de seguridad de esta caja. Algunos de estos conflictos son los siguientes:
- Balance vs no linealidad [2]: Se ha demostrado que cajas la mejor no linealidad no pueden ser balanceadas.
- CarL1 vs uniformidad diferencial [25]: CarL1 es una propiedad para cifradores con una capa de permutación de bit. Esta propiedad es importante para lograr la difusión. Sin embargo, el mejor valor que presenta esta propiedad cuando n = m = 4 (CarL1=1) ocasiona que la uniformidad no logre el valor óptimo (que es 4).
Debido a los diferentes conflictos, algunos trabajos buscan mejorar algunas propiedades de la caja S mientras analizan otras propiedades que se pueden alterar [26]. A su vez, se buscan proponer nuevos compromisos para tratar de lograr un nivel de seguridad balanceado entre las propiedades [17], [27].
B. Cajas S para cifradores ligeros
Un cifrador ligero está orientado a ser implementado en dispositivos que tienen recursos limitados, tales como los dispositivos IoT [1]. Este tipo de cifradores requieren que la caja sea de un tamaño más pequeño, en otras palabras una caja se considera ligera si 3 ≤ n,m ≤ 8. Una caja más pequeña ocupara menos recursos del dispositivo para proveer los principios de confusión y difusión. No obstante, ésta no logrará el mismo nivel de seguridad que las cajas grandes. Por lo tanto, la búsqueda de cajas ligeras sigue siendo un problema en donde se debe considerar el compromiso entre la seguridad y el costo [28].
C. Enfoques de construcción
Existen diversos enfoques de construcción para la caja como el algebraico [3], heurístico [26] y la búsqueda aleatoria [9]. A pesar de que el enfoque algebraico ha logrado encontrar las mejores cajas debido a la alta resitencia que presentan ante los ataques ataques criptográficos, este tipo de construcción revela ser suceptible ante los ataques algebraicos [4]. Con base a esto, la mejora y la propuesta de nuevos enfoques de construcción es necesaria para cubrir esta vulnerabilidad.
VII. CONCLUSIÓN
Las cajas S son muy importantes para proveer la confusión y difusión en los cifradores. Este trabajo presenta de forma general la importancia de esta función para crear los mensajes cifrados, la definición de este componente, la relación entre ataques y propiedades, y su nivel de seguridad. A su vez, se muestra algunos de los problemas actuales relacionados a la búsqueda de una caja S como la propuesta de compromisos entre las propiedades y el diseño de cajas S para cifradores ligeros.
El estudio de estas cajas conlleva una complejidad matemática que puede resultar desafiante para entender los conceptos relacionados con el tema. Por consiguiente, este trabajo busca servir como una referencia accesible para el lector, de modo que pueda profundizar en el estudio de este tema.
Footnote
1AES es un cifrador estandarizado por el NIST (siglas de National Institute of Standards and Technology) desde el 2001.
REFERENCIAS
- [1] G. Hatzivasilis, K. Fysarakis, I. Papaefstathiou, and C. Manifavas, “A review of lightweight block ciphers,” Journal of cryptographic Engineering, vol. 8, pp. 141–184, 2018.
- [2] Z. Bao, J. Guo, S. Ling, and Y. Sasaki, “Sok: Peigen – a platform for evaluation, implementation, and generation of s-boxes.” Cryptology ePrint Archive, Paper 2019/209, 2019. https://eprint.iacr.org/2019/209.
- [3] J. Daemen and V. Rijmen, AES proposal: Rijndael. Gaithersburg, MD, USA, 1999.
- [4] N. T. Courtois and J. Pieprzyk, “Cryptanalysis of block ciphers with overdefined systems of equations,” in Advances in Cryptology—ASIACRYPT 2002: 8th International Conference on the Theory and Application of Cryptology and Information Security Queenstown, New Zealand, December 1–5, 2002 Proceedings 8, pp. 267–287, Springer, 2002.
- [5] C. Paar and J. Pelzl, Understanding cryptography, vol. 1. Springer, 2010.
- [6] C. E. Shannon, “Communication theory of secrecy systems,” The Bell system technical journal, vol. 28, no. 4, pp. 656–715, 1949.
- [7] T. Suzaki, K. Minematsu, S. Morioka, and E. Kobayashi, “Twine: A lightweight, versatile block cipher,” in ECRYPT workshop on lightweight cryptography, vol. 2011, Springer Berlin, Heidelberg, 2011.
- [8] C. Dobraunig, M. Eichlseder, F. Mendel, and M. Schl¨affer, “Ascon v1. 2: Lightweight authenticated encryption and hashing,” Journal of Cryptology, vol. 34, pp. 1–42, 2021.
- [9] T. Shirai, K. Shibutani, T. Akishita, S. Moriai, and T. Iwata, “The 128-bit blockcipher clefia,” in Fast Software Encryption: 14th International Workshop, FSE 2007, Luxembourg, Luxembourg, March 26-28, 2007, Revised Selected Papers 14, pp. 181–195, Springer, 2007.
- [10] Z. Bao, J. Guo, S. Ling, and Y. Sasaki, “Peigen – a platform for evaluation, implementation, and generation of s-boxes,” 2019. Accessed: September 27, 2024.
- [11] L. Li, J. Liu, Y. Guo, and B. Liu, “A new s-box construction method meeting strict avalanche criterion,” Journal of Information Security and Applications, vol. 66, p. 103135, 2022.
- [12] W. Zhang, Z. Bao, D. Lin, V. Rijmen, B. Yang, and I. Verbauwhede, “Rectangle: a bit-slice lightweight block cipher suitable for multiple platforms,” Cryptology ePrint Archive, 2014.
- [13] C. De Canniere, A. Biryukov, and B. Preneel, “An introduction to block cipher cryptanalysis,” Proceedings of the IEEE, vol. 94, no. 2, pp. 346–356, 2006.
- [14] J. Lim, D. Ng, and R. Ng, “Sok: Security evaluation of sbox-based block ciphers,” Cryptology ePrint Archive, 2022.
- [15] M. Stamp and R. M. Low, Applied cryptanalysis: breaking ciphers in the real world. John Wiley & Sons, 2007.
- [16] C. Carlet, “Boolean functions for cryptography and coding theory,” 2021.
- [17] W. Zhang, Z. Bao, V. Rijmen, and M. Liu, “A new classification of 4-bit optimal s-boxes and its application to present, rectangle and spongent,” in Fast Software Encryption: 22nd International Workshop, FSE 2015, Istanbul, Turkey, March 8-11, 2015, Revised Selected Papers 22, pp. 494–515, Springer, 2015.
- [18] Y. Tong, S. Xu, J. Huang, B. Wang, and Z. Ren, “A new analysis of small s-boxes based on a new notion of algebraic immunity,” Journal of Information Security and Applications, vol. 77, p. 103574, 2023.
- [19] D. E. Standard et al., “Data encryption standard,” Federal Information Processing Standards Publication, vol. 112, p. 3, 1999.
- [20] G. Orhanou, S. El Hajji, and Y. Bentaleb, “Snow 3g stream cipher operation and complexity study,” Contemporary Engineering Sciences-Hikari Ltd, vol. 3, no. 3, pp. 97–111, 2010.
- [21] M. B. Farah, R. Guesmi, A. Kachouri, and M. Samet, “A new design of cryptosystem based on s-box and chaotic permutation,” Multimedia Tools and Applications, vol. 79, pp. 19129–19150, 2020.
- [22] K. Nyberg, “Differentially uniform mappings for cryptography,” in Workshop on the Theory and Application of of Cryptographic Techniques, pp. 55–64, Springer, 1993.
- [23] D. R. Stinson, Cryptography: theory and practice. Chapman and Hall/CRC, 2005.
- [24] T. S. Developers, SageMath, the Sage Mathematics Software System (Version 9.6), 2022. https://www.sagemath.org.
- [25] L. Cheng, W. Zhang, and Z. Xiang, “A new cryptographic analysis of 4-bit s-boxes,” in Information Security and Cryptology: 11th International Conference, Inscrypt 2015, Beijing, China, November 1-3, 2015, Revised Selected Papers 11, pp. 144–164, Springer, 2016.
- [26] M. Durasevic, D. Jakobovic, L. Mariot, S. Mesnager, and S. Picek, “On the evolution of boomerang uniformity in cryptographic s-boxes,” in International Conference on the Applications of Evolutionary Computation (Part of EvoStar), pp. 237–252, Springer, 2023.
- [27] G. Leander and A. Poschmann, “On the classification of 4 bit s-boxes,” in Arithmetic of Finite Fields: First International Workshop, WAIFI 2007, Madrid, Spain, June 21-22, 2007. Proceedings 1, pp. 159–176, Springer, 2007.
- [28] D. C. Ventura, L. M. R. Henríquez, and S. E. P. Hernández, “Requirements for feistel-based lightweight block cipher s-boxes to be resilient to boomerang attacks,” in 2023 Mexican International Conference on Computer Science (ENC), pp. 1–8, 2023.
- ISSN: 3061-8991
- Vol 1, 2025